Don't hammer the charge particle , he is innocent !
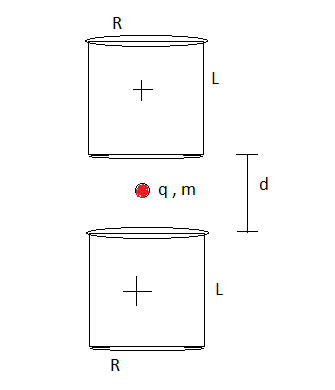 Consider two fixed identical uniformly charged solid cylinder's having volume charge density
and radius
length
each and separated by distance
. If a point charge is kept at a mid point of these cylinder on their axis, so that system is in equilibrium. Then find time period of small vertical oscillation of charged particle. If it expressed as:
Consider two fixed identical uniformly charged solid cylinder's having volume charge density
and radius
length
each and separated by distance
. If a point charge is kept at a mid point of these cylinder on their axis, so that system is in equilibrium. Then find time period of small vertical oscillation of charged particle. If it expressed as:
Find least value of
Details and assumptions :
-
-
is permittivity of free space and neglect gravity.
Original !
Try more Deepanshu's mixing of concepts
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First we need to evaluate the electric field by a cylinder of uniform charge density ρ , length L and radius R at a point on its axis . This can be found by integrating over elemental discs . I will leave the integration part and and only give the final result here .
E = 2 ϵ ρ ( L − ( d + L ) 2 + R 2 + d 2 + R 2 ) ........ where d is the distance of the point from the base of the cylinder closer to it
Consider the state of the particle when it is displaced by a small distance x from its mean position
The net electric field acting on the particle is
E = 2 ϵ ρ ( ( ( 2 d + x + L ) 2 + R 2 − ( 2 d − x + L ) 2 + R 2 ) − ( ( 2 d + x ) 2 + R 2 − ( 2 d − x ) 2 + R 2 ) )
grouping the terms as shown above and after substituting the values given and simplifying using the binomial approximation ( ( 1 + x ) n ≈ 1 + n x , for x < < 1 ) , we get
E = 1 0 ϵ ρ x ( 4 5 − 5 2 )
the acceleration of the charged particle will be
a = m q E
Comparing with standard equation for S . H . M a = ω 2 x , we get
ω = 1 0 m ϵ ρ q ( 4 5 − 5 2 )
Thus time period of oscillation is
T = 2 π 3 ρ q ( 4 5 + 5 2 ) m ϵ
∴ a = 4 , b = 5 , c = 5 , d = 2 , e = 3
Hence the answer is 1 9