Don't look down
A 80 kg climber is standing horizontally on a perfectly vertical cliff face as shown in the picture. The climber is 1.8 meters tall and is attached by a 2-meter-long rope fastened around the climber's middle to a point on the cliff above him. What is the normal force the cliff face exerts on the climber in Newtons ?
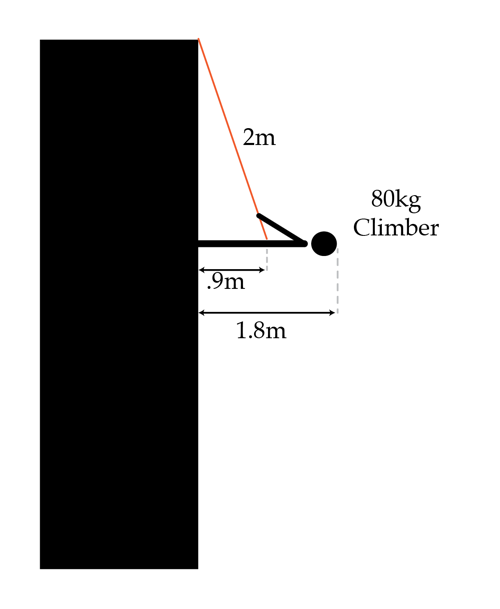
Details and assumptions
- The climber is not moving.
- The acceleration of gravity is − 9 . 8 m/s 2 .
- The center of mass of the climber is at the point where the rope meets their body.
The answer is 395.06.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Let the mass of man be m. Then mg force is acting vertically downwards from the center of mass. Let the normal force be N acting horizontally towards the right from the point of contact of the man and the wall. Breaking the tension into perpendicular components along vertical and horizontal direction and balancing the forces we get: TsinA=mg A being the angle the rope makes with the man TcosA=N dividing both equation we get tanA=mg/N N=mg/tanA N=395.060
First let us know and count the total forces acting on the climber. (m=80 kg, g=9.8 m/s^2 downwards) Let, W= mg = Force of gravity(gravitational pull acting downwards from centre of mass), T= Tension due to rope(acting along the rope in upwards direction), N= Normal force exerted by cliff on climber(in direction perpendicular to plane of cliff towards climber). Also let ' \theta ' be the vertical angle between rope and the cliff. Clearly on resolving the forces(and as climber is at rest,the net force on body is zero). Hence, W - T cos \theta = 0 , mg= T cos \theta ....eqn(1). and, N - T sin \theta = 0 , N= T sin \theta ....eqn(2). Dividing eqn(1) by eqn(2),we get, N= mg tan \theta .....eqn(3). Now tan \theta can be easily obtained using pythagoras theorem and trigonometry, that comes out tan \theta = 0.5039. Hence from eqn(3), N= (80)x(9.8)x(0.5039) = 395.0576 Newtons. Rounding off,we get, N = 395.06 Newtons.
Let us consider the free body diagram of the climber. The list of forces on the centre of mass are:-
1) Normal 'N' towards right.
2) Weight 'W' downwards.
3) Tension 'T' at some angle say 'theta' between the climber and the rope in clockwise direction.
Now, since the system is in equilibrium, hence, all the forces both in the vertical and the horizontal direction will balance.
Hence, balancing vertical direction, W=T x sin(theta) => T = W/sin(theta)
Also, balancing horizontal direction, N=Txcos(theta) =>N = W x cot(theta)
Calculating theta by simple trigonometry, we get cot(theta)=0.5039 and calculating W = mass x 9.8 = 80 x 9.8 = 784 Hence, by putting in the values, we get N = 784 x 0.504 = 395.06
Since the center of mass of the climber is at the point where the rope meets the body, and the climber is horizontal, both the normal force the climber experience from the wall and the tension force passes through the center of mass. So we can neglect any rotation and simply treat the climber as a point mass. Let θ be the angle the rope makes with the wall. The weight acting on the climber must be exerted entirely by the tension T from the rope, as the normal force from the wall is perfectly horizontal. Which gives us the equation T cos θ = m g where m = 8 0 k g and g = 9 . 8 1 The normal force would simply be the horizontal component of the tension T , given by T sin θ From trigonometry, we know that sin θ = 2 0 9 After some basic trigonometry, we rearrange the equation to be T sin θ = T cos θ × tan θ . Substituting θ = arcsin 2 0 9 gives 395 to 3 significant figures.
Since the climber is in equilibrium the forces in the x and y directions are balanced. We therefore have
F x = − T s i n θ + N = 0
F y = T c o s θ − m g = 0
where T is the tension, N is the normal force, θ is the angle the rope maxes with the vertical. We can solve this system of equations for N=395.06 N.
Draw a free-body diagram and divide the problem up into the x -component and y -component. Let θ be the angle between the red wire and the horizontal person. Let T be the tension - going "up the wire". Let N be the desired normal force, at the pivot of the person's foot and facing up the person's body (rightwards in the picture). Also, let m g be the person's weight.
Then, the y -component part of Newton's Second Law gives us: T sin θ = m g . Similarly, the x -component part gives us: N = T cos θ . We want N . Note that, from the first equation, we have: T = sin θ m g . Substituting this into the second equation, we have: N = sin θ m g cos θ = m g cot θ . Note, however, that we have a right triangle from which we can get θ . By some quick Pythagorean Theorem, we find that the "missing leg" of the triangle is 1.786 m. So, we can find cot θ quite easily. Substitute this value and m = 8 0 kg and g into the equation, and multiply, to get: N = 3 9 5 N .
Remark : Using torques and setting the net torque equal to 0 , we would have gotten the same thing.