Don't Multiply It Out!
Find the remainder when 3 2 0 1 5 + 7 2 0 1 5 is divided by 50.
This problem is part of the set AMSP .
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Moderator note:
I was thinking of Chinese Remainder Theorem. But this gets the job done fairly quick as well. Nice!
mod 2 5 : 3 2 0 1 5 ( m o d 2 0 ) + 7 2 0 1 5 ( m o d 2 0 ) by Euler's theorem.
≡ 3 − 5 + 7 − 5 ≡ 6 8 1 ⋅ 3 1 + ( − 1 ) 2 4 9 2 ⋅ 7 1 ≡ 1 8 1 + 7 1 ≡ − 7 1 + 7 1 ≡ 0 and clearly is even, so divisible by 5 0 too.
3 2 0 1 5 + 7 2 0 1 5 ≡ [ ( 3 5 ) 4 0 3 + ( 7 5 ) 4 0 3 ] ( m o d 5 0 ) ≡ [ 2 4 3 4 0 3 + 1 6 8 0 7 4 0 3 ( m o d 5 0 ) ≡ [ ( − 7 ) 4 0 3 + ( 7 ) 4 0 3 ] ( m o d 5 0 ) ≡ 0 ( m o d 5 0 )
The last digit of 3^2015 will be 7.
The last digit of 7^2015 will be 3.
Hence the last digit of the sum will be 0.
Hence it will be completely divisible by 50.
Moderator note:
As Aalap Shah has pointed out, you did not prove that it can further be divisible by 5.
No, this only ensures divisibility by 10, not 50.
Perfect website: https://www.mtholyoke.edu/courses/quenell/s2003/ma139/js/powermod.html
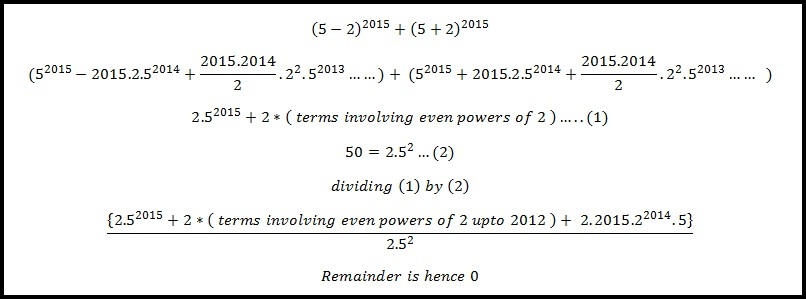
3 2 0 1 5 + 7 2 0 1 5 ≡ ( 3 5 ) 4 0 3 ( m o d 5 0 ) + 7 ( 7 2 ) 1 0 0 7 ( m o d 5 0 ) ≡ [ ( 2 4 3 ) 4 0 3 + 7 ( 4 9 ) 1 0 0 7 ] ( m o d 5 0 ) ≡ [ ( − 7 ) 4 0 3 + 7 ( 5 0 − 1 ) 1 0 0 7 ] ( m o d 5 0 ) ≡ [ − 7 ( 4 9 ) 2 0 1 + 7 ( − 1 ) ] ( m o d 5 0 ) ≡ [ − 7 ( − 1 ) + 7 ( − 1 ) ] ( m o d 5 0 ) ≡ 0 ( m o d 5 0 )