Don't resist it! (2)
The cube in the figure is made of 12 wire segments of 1 Ω resistance each.
Find the overall resistance between vertices A and B .
The answer is 0.58333333.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
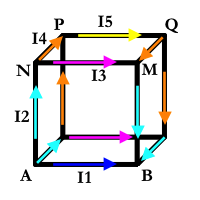
Using the symmetry of the cube with respect to side A B , we can deduce that there are five different intensities (colors) we have to relate.
We now apply Kirchhoff's laws of nodes and closed loops to build enough equations to find them:
Node A: Node N: Node P: Loop NPQM: Loop ANMB: I T I 2 I 5 I 3 I 1 = = = = = I 1 + 2 I 2 I 3 + I 4 2 I 4 2 I 4 + I 5 2 I 2 + I 3
We get: I 5 = 2 I 4 ; I 3 = 4 I 4 ; I 2 = 5 I 4 ; I 1 = 1 4 I 4 ; I T = 2 4 I 4
R = I T V A B = I T 1 Ω ⋅ I 1 = 2 4 I 4 1 4 I 4 = 1 2 7 Ω
Label the cube circuit as shown in the left figure. By symmetry, the three vertices adjacent to A , C ′ and C ′ ′ have the same voltage with respect to A and B . Therefore, C ′ and C ′ ′ can be considered as a point C . Similarly, the three vertices adjacent to B , D ′ and D ′ ′ can be considered as a point D . Then the equivalent circuit of the cube circuit is as the right figure. And the resultant resistance between A and B is given by:
R A B = ( r A C + r C D + r D B ) ∣ ∣ r A B = ( 1 ∣ ∣ 1 + 1 ∣ ∣ ( 1 ∣ ∣ 1 + 1 + 1 ∣ ∣ 1 ) ∣ ∣ 1 + 1 ∣ ∣ 1 ) ∣ ∣ 1 = ( 2 1 + 1 ∣ ∣ ( 2 1 + 1 + 2 1 ) ∣ ∣ 1 + 2 1 ) ∣ ∣ 1 = ( 2 1 + 1 ∣ ∣ 2 ∣ ∣ 1 + 2 1 ) ∣ ∣ 1 = ( 2 1 + 5 2 + 2 1 ) ∣ ∣ 1 = 5 7 ∣ ∣ 1 = 5 7 + 1 5 7 × 1 ≈ 0 . 5 8 3