Don't Spill it!

Geometry Level 4

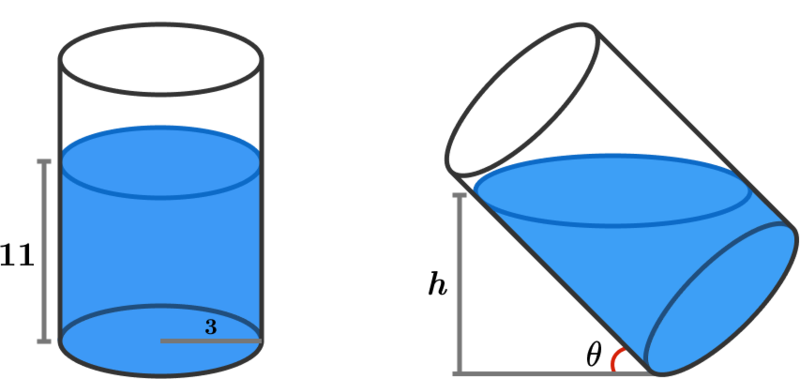
A cylindrical glass of radius 3 is filled with water until its height reaches 11, as shown above left.

Now, if the cylinder is tilted such that it forms an angle of $\theta$ with the ground with $\cos \theta = \frac{4}{5}$ , what is the new height $h$ ?

Clarification: The cylinder is so long that no water spills over.

The answer is 9.

1 solution

Worranat Pakornrat
Mar 4, 2017

According to Shadow Blocks , we have learnt that the cut section of the same volume would have the same area. That is, the average oblique lengths would equal to $11$ , the original height, and we can set $x$ as the excess length to the glass' rim as shown below:

If $\cos \theta = \dfrac{4}{5}$ , then $\sin \theta = \dfrac{3}{5}$ and $\tan \theta = \dfrac{3}{4}$ .

Then $\tan \theta = \dfrac{3}{4} = \dfrac{radius}{x}$ . Thus, $x = 4$ .

Hence, $\sin \theta = \dfrac{3}{5} = \dfrac{h}{x+11} = \dfrac{h}{15}$ . Thus, $h = \boxed{9}$ .

"According to Shadow Blocks, we have learnt that the cut section of the same volume would have the same area."

It's called Cavalieri's Principle if you don't know.

Still a nice problem

Jason Chrysoprase - 4 years, 3 months ago

Well, I know. Still I think it's easier to compare similar problems. ;)

Worranat Pakornrat - 4 years, 3 months ago

Don't Spill it!

The answer is 9.

1 solution

0 pending reports