Don't Think Outside The Box!
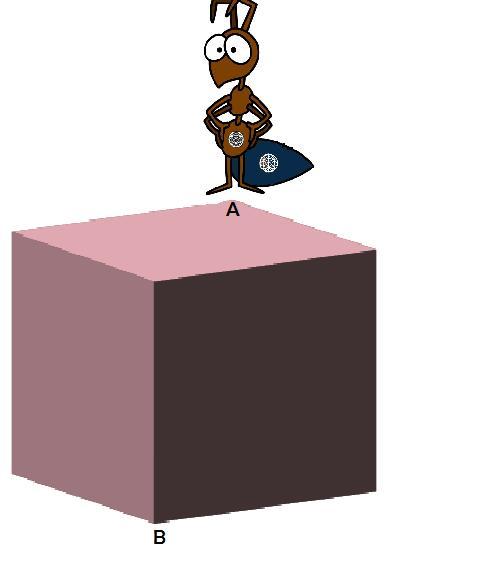 Brilli the ant is trapped on a cube-shaped planet. She wants to go from one corner [point
A
] to the opposite corner [point
B
]. However she wants do this in a way such that she has to cross the shortest distance possible. If the length of the sides of the cube is
1
, the shortest distance between
A
and
B
can be expressed as
p
+
q
where
p
and
q
are non-negative integers and
q
is square-free. What is
q
−
p
?
Brilli the ant is trapped on a cube-shaped planet. She wants to go from one corner [point
A
] to the opposite corner [point
B
]. However she wants do this in a way such that she has to cross the shortest distance possible. If the length of the sides of the cube is
1
, the shortest distance between
A
and
B
can be expressed as
p
+
q
where
p
and
q
are non-negative integers and
q
is square-free. What is
q
−
p
?
Details and assumptions :
Brilli the ant is completely confined to the surface of the cube. She can't move inside or outside the cube.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Ugh, I was pondering for 5 minutes why 5 wasn't the answer, then I realized it was, because p = 0 . Trippy.
Log in to reply
A common wrong answer is 1 + 2 . That's why I put p + q as the format.
I was also hesitant while entering 5 . And I had to recheck all over again, cause of the format of the answer
Exactly! It's so throw-y off-y! :O
This is a famous problem created by Henry Ernest Dudeney From The Canterbury Puzzles 1908. The original problem is called the Spider and the Fly Problem. http://mathworld.wolfram.com/SpiderandFlyProblem.html
really out of box.....
i assumed she could move on the edge of the box so my answer came out to be 1 instead
Log in to reply
She can, but she wants to cover the shortest distance possible and that doesn't happen when she moves along the edges.
Sorry , its"down the edge to B".
Wait a minute you said ant is trapped on planet so how are you unfolding it.ant will have to travel on diagonal line of upper surface and then down the edge to point A.so answer is 1+2^(1/2).now 2-1=1.
Log in to reply
She is trapped! She is confined to the surface of the cube.
It's easier to visualize the whole thing when you unfold it. But Brilli's path is still along the surface of the cube for this solution.
See the shortest distance should be sqrt(2)+1
Here is a very similar problem by me, Cupid the Caterpillar . As @Mursalin Habib mentioned, drawing a net is the easiest possible way.
Try opening up the cube like this:
It is apparent that the shortest distance between A and B is 2 2 + 1 2 = 5 .
That means p = 0 and q = 5 and q − p = 5 − 0 = 5 .