Don't try experimenting it

For the purposes of calculations an ideal voltage source in electrical series with an internal resistor can be substituted for an actual battery. In a battery there is an internal resistance that is a result of the construction of the battery and cannot be separated from the voltage source.

In a series circuit, the current that flows through each of the components is the same, and the voltage across the circuit is the sum of the individual voltage drops across each component

Note; the voltmeter is assumed to have a vey high impedance and therefore is not a factor in the calculations

Ohms law I=V/R. or V=IR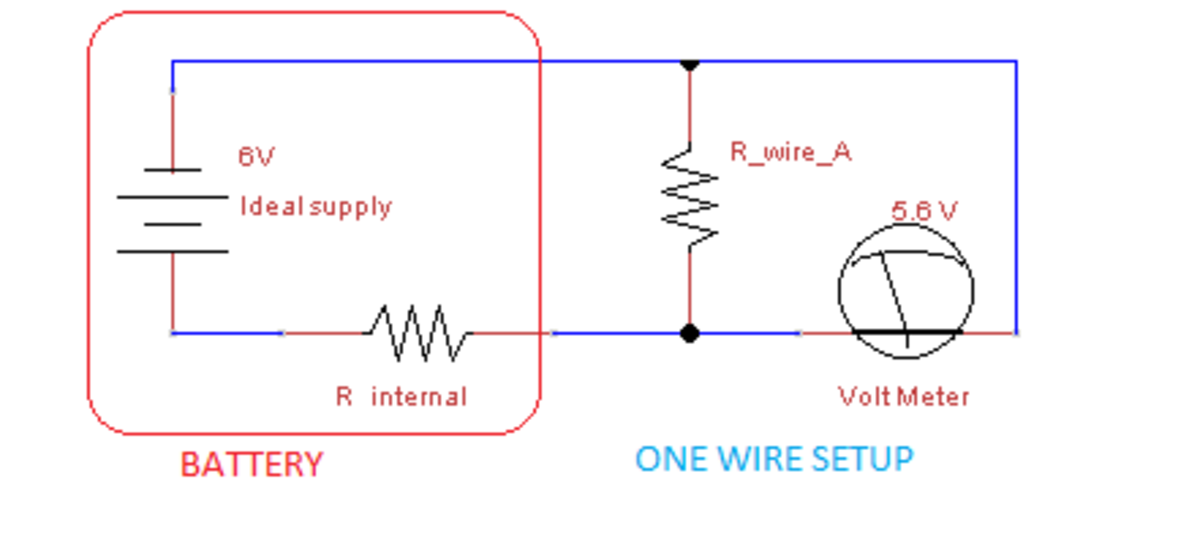

Setup with one wire.

${ V }_{ sup }={ V }_{ Rint }+{ V }_{ RwireA }\\ { V }_{ Rint }=6-5.6=0.4V\\ { I }_{ Rint }={ I }_{ RwireA }\\ \frac { { V }_{ Rint } }{ { R }_{ int } } =\frac { { V }_{ RwireA } }{ { R }_{ wireA } } \\ \frac { { R }_{ int } }{ { R }_{ wireA } } =\frac { 5.6 }{ 0.4 } =14\\ { R }_{ int }=14{ R }_{ wireA }$

Setup with two wires.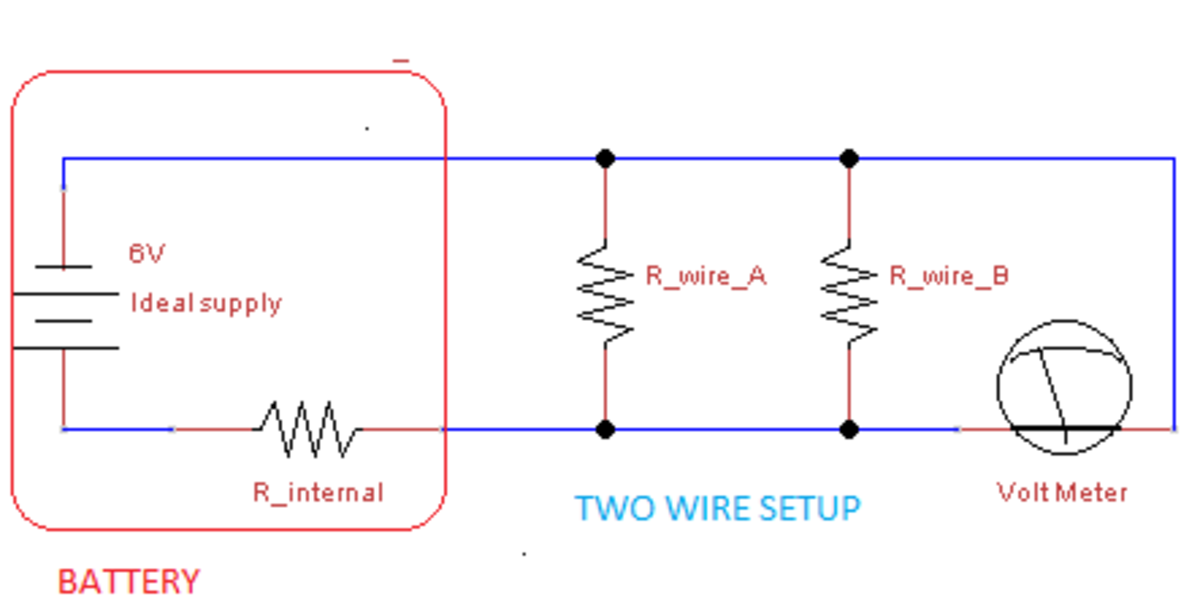

Wire A is in parallel with wire B.

${ R }_{ A }={ R }_{ B }\\ \frac { 1 }{ { R }_{ A||B } } =\frac { 1 }{ { R }_{ A } } +\frac { 1 }{ { R }_{ B } } =\frac { 1 }{ 2{ R }_{ A } } \\ { R }_{ A||B }=\frac { 1 }{ 2 } { R }_{ A }\\ { R }_{ A||B }=7{ R }_{ int }$

Resistance of the wires A || B are in series with the battery’s internal resistor.

The voltage drop across the internal resistance of the battery + the voltage drop across the two wires in parallel equal 6 volts of the supply.

${ R }_{ total }={ R }_{ int }+{ R }_{ A||B }\\ { R }_{ total }={ 8R }_{ int }\\ { R }_{ A||B }=\frac { 7 }{ 8 } { R }_{ total }$

The voltage drop is proportional to the resistances.

${ V }_{ total }={ V }_{ Rint }+{ V }_{ R\_ A||B }\\ { V }_{ total }={ V }_{ int }=6V\\ { V }_{ A||B }=\frac { 7 }{ 8 } { V }_{ total }=\frac { 7 }{ 8 } 6=5.25V$