I love Threes!
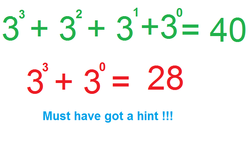 How many positive integers less than or equals to
1
0
0
cannot be written as the sum of distinct powers of
3
?
How many positive integers less than or equals to
1
0
0
cannot be written as the sum of distinct powers of
3
?
The answer is 77.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Hey, I thought that 1, 3, 9 ,27 and 81 count because they arent a sum of powers of 3! you may want to espicify that!
I wasn't sure whether or not to include 0 in the set of numbers that cannot be represented as such. I first assumed that at least one power of 3 had to be summed, implying that 0 could not be represented and hence my first guess of 78 was incorrect. I think it might be less confusing if you just ask "How many positive integers ....." instead. Just a suggestion; good question otherwise. :)
Log in to reply
Ok, that is also fine .... But in my solution, then we'll have to discard the case of 0 0 0 0 i.e. 0, hence the answer will just be like 1 number is removed from superset and same number is removed from subset, making no change to the answer, so I prefer keeping it like this only :) Thanks for the suggestion though ! Regards, - Aditya Raut
hey i did it this way , distinct powers of three = 0 , 1 , 2 , 3 , 4 which leads us to numbers 1 , 3 , 9 , 27 , 81 now we have to make sets of minimum two elements such that their sum is less than 100 .. i found 17 such sets by applying combination method, thus my ans. is 83 . what is wrong in it.
Log in to reply
You have five powers of 3 as a choice. We see that if you take 27 and 81 together, sum exceeds 100. Thus you have to leave the cases in which 81 and 27 are there simulaneously and such there will be 8 cases. (because other powers are total 3). Hence out of all the posibilities of the sum (which is 2^5 because each power either can be or can't be in thesum)
Hence you had 32 total sums possible and out of them 8 you reduced bcoz they had 81 and 27 together, so what remains is 0, so reduce that too, resulting in 23 numbers of type not asked, total are 100, so removing these 23 gives 77 as the answer.
But you have mentioned positive integers . Is 0 a positive integer?
You spelt distinct wrong. I see you got my report. I originally tried 0 because you hadn't written.
please explain more
can any one explain in a better way
If we write numbers as base 2 with 5 digits such that 1 in digit n (from right to left) has the value of 3 n − 1 . (Ex. 1 0 1 1 0 = 3 4 + 3 2 + 3 1 )
We get 0 0 0 0 1 , 0 0 0 1 0 , 0 0 0 1 1 , 1 0 1 1 1 ( max ) .
Now it's the job of combinatorics to count those numbers. 2 5 − 2 3 − 1 = 2 3 .
Therefore, the number of positive integers from 1 to 1 0 0 that doesn't satisfy that = 1 0 0 − 2 3 = 7 7 ~~~ Meow!!!
Note:
There're 2 choices for 5 digits, 2 5 .
For 1 1 ∗ ∗ ∗ . It's impossible because 3 4 + 3 3 > 1 0 0 . Subtract 2 3 .
For 0 0 0 0 0 . Doesn't satisfy. Subtract 1.
Number of ways = 2 5 − 2 3 − 1 = 2 3 . ~~~
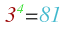 is the highest power of 3 that can be present. So the given task boils down to the following problem. For a given equation
is the highest power of 3 that can be present. So the given task boils down to the following problem. For a given equation
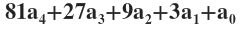
we have to find all possible combinations of values of
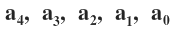
Here all the
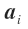 can only have two possible values 0 or 1.
can only have two possible values 0 or 1.
Solution:

5 nos. possible 3^0 3^1 3^2 3^3 3^4
Take 4 nos. 3^(0,1,2,3).
No of ways they can form a no. = 2^4 -1=15
(-1 for 0)
Take next 4 nos. 3^(0,1,2,4).
No of ways they can form a no. = 2^4 -1=15
Remove common nos. 3^(0,1,2).
No of ways they can form a no. = 2^3 -1=7
Total no of ways a no. cannot be formed = 15+15-7=23
My solution is based on combinatorics. Here it goes: Powers of 3 which can be considered (satisfying the given conditions): 0,1,2,3,4.... (5 distinct values)...... We can choose 1 or 2 or 3 or 4 values at a time.. (can't choose 0 values or 5 values(>100) ) So, 5C1+5C2+5C3+5C4 = 2^5-2 = 30 ...... Now the only thing that remains is to eliminate "selections" that do not satisfy the condition (natural no < 100)... observe all such selections will contain 81 (the largest power ... closest to 100)... For 1 selection: 0 For 2 selection: 1 (81,27) For 3 selection: 3 (81,27,x) ... x= {1,3,9} For 4 selection: 3 (81,27,x,y) ... x,y = {1,3,9} and x not= y So total no of valid selections = 30-(1+3+3)=23 .... (each selection results in a unique natural no. as all constituent elements are +ve and distinct..) So, numbers which cannot be formed 100-23 = 77 values
Hope this helps :-)
It would be much better it you typed in LaTeX.
I probably did this the hard way, and also couldn't figure out how to write choose in the text editor, but here goes. So you know that the largest power of 3 you can have is 3 4 = 8 1 . Next largest is 2 7 , 9 , 3 . 1 . Now we can't add 2 7 to 8 1 because it will be greater than 1 0 0 . So we can only add combinations of 9 , 3 , and 1 to 8 1 . So we have 8 1 + 3 choose 1 + 3 choose 2 + 3 choose 3. 2 7 can't be added to 8 1 , but can be added to combinations of 9 , 3 , and 1 so we have 2 7 + 3 choose 1 + 3 choose 2 + 3 choose 3. likewise we have 9 + 2 choose 1 + 2 choose 2, and finally we have 3 + 1 choose 1. All we do is total up the number of combinations and we get 2 3 , so 1 0 0 − 2 3 = 7 7
The bases solution was already very good. However, if you, like me, don't like working with bases, then you can use this solution. Considering just 1, 3, 9, and 27, we can choose any combination of them to sum up, because the total sum is less than 100. Using set theory, the number of ways is 2 4 = 1 6 . Note that this also includes the null set. Therefore, there are actually 15 ways.
Now, including 81, we have to have a sum of any combination of 1, 3, 9, and 27 that is ≤ 1 9 . 27 can't be used, but any combination of 1, 3, and 9 can be used because 9 + 3 + 1 = 1 3 ≤ 1 9 . Using set theory again, we have 2 3 = 8 . This time, the null set can be used as we are adding to 81. Therefore, the total possible combinations is 1 5 + 8 = 2 3 , and the answer is 7 7 .
There are 101 non-negative integers less than or equal to 100.
If you want a number to be sum of powers of 3 , then it's representation in base 3 can have only the digits 0 and 1 .
Observe that the maximum power of 3 less than 100 is 4. ( 3 4 = 8 1 < 1 0 0 )
Thus the representation of our numbers (all numbers till 100) can be of maximum length of 5 digits !
For example, 2 8 = 1 0 0 1 in base 3, so it's 3 3 + 3 0 .
In our base 3 representation if it's 4 digit and the number can be written as sum of powers of 3, then it can at the max be 1 1 1 1 3 = 2 7 + 9 + 3 + 1 = 4 0 (in base 10)
Thus all the numbers which have only 0 or 1 in their respective base 3 representation are at max 4 digit are to be firstly counted .
All the 4 digits have 2 choices (0 or 1) so there will be 2 4 = 1 6 numbers which have at the max 4 digit representation in base 3 ( 0 is also included).
What remains to count is numbers which have only 0 or 1 in the base 3 representation and are 5 digit long. They are 1 0 0 0 0 , 1 0 0 0 1 , 1 0 0 1 0 , 1 0 0 1 1 , 1 0 1 0 0 , 1 0 1 0 1 , 1 0 1 1 0 , 1 0 1 1 1 which are 8 1 , 8 2 , 8 4 , 8 5 , 9 0 , 9 1 , 9 3 , 9 4 respectively in base 10, giving 8 more numbers.
Hence we have 24 numbers less than 100 which can be written as sums of powers of 3. Thus out of the total 101 numbers, the 24 are reduced , hence there'll be 1 0 1 − 2 4 = 7 7 numbers.