DON'T USE A CALCULATOR !!!!!
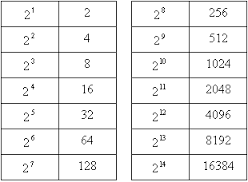 WHAT IS THE VALUE IF WE ADD ALL THESE NUMBERS UP TO 2 ^ 13
WHAT IS THE VALUE IF WE ADD ALL THESE NUMBERS UP TO 2 ^ 13
The answer is 16382.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
a = 2, r = 4/2 = 2
S
n
=
r
−
1
a
(
r
n
−
1
)
S
1
3
=
2
−
1
2
(
2
1
3
−
1
)
= 2 x (8392-1)
= 2 x 8391
=
1
6
3
8
2
*I 'm sorry for bad formatting. Maybe someone can help me to tidy up my formatting.
Simply solved as this ia an G.P. and we can simply use the expression of sum of GP.......... Yeah. :)
It's a GP.Not an AP.
Log in to reply
Sorry for that . Yeah it's a g.p.
Dude its GP
We will prove that ∑ k = 0 n 2 k = 2 k + 1 − 1 using induction.
Base Case;
When k = 0 , ∑ k = 0 n 2 k = 2 0 = 1 = 2 − 1 = 2 1 − 1
Inductive Step
Assume that ∑ k = 0 n 2 k = 2 k + 1 − 1 for some k ∈ Z
We will prove that (\sum _{ k=0 }^{ n }{ { 2 }^{ k+1 } } ={ 2 }^{ k+2 }-1).
Multiplying the assumption by 2,
2 ⋅ 2 0 + 2 ⋅ 2 1 + . . . + 2 ⋅ 2 k = 2 k + 2 − 2
Adding 1 to both sides,
1 + 2 1 + 2 2 + . . . + 2 k + 1 = 2 k + 2 − 1
So ∑ k = 0 n 2 k + 1 = 2 k + 2 − 1 .
So we have the conclusion, and the answer is 2 1 4 − 1 = 1 6 3 8 3 □
Thanks. I have updated the answer to this problem.
The slight mistake made in this solution is starting with k = 0 , whereas the problem starts with k = 1 .
I see the problem can be solved using geometric progression: http://en.wikipedia.org/wiki/Geometric_progression. Sum will be 16382.
Log in to reply
Yup!! I solved it using Geometric Progression as well...and the sum comes out to be 16382 @Calvin Lin Please check it...
in PHP:
1 2 3 4 5 6 7 8 |
|
..but if we would utilize the values in the table given, we could see a pattern and come up with a formula for the summation of 2^n.
X = (2^(n+1)) - 2
where n = 13
X = (2^(13+1))-2
X = (2^14)-2
X = 16384-2
X = 16382
Stop writing in all caps. It hurts my eyes.
just subtract two from value 2^14
I honestly just added them all. EDIT:I have actually found a way to do this!!! 2 k − 1 = ( 2 − 1 ) ( 2 k − 1 + 2 k − 2 + ⋯ + 2 1 + 1 ) 2 k − 1 = 2 k − 1 + 2 k − 2 + ⋯ + 1 Insert k=14.The R.H.S becomes: 2 1 3 + 2 1 2 + ⋯ + 1 In order for this to become the series we want, we have to subtract 1.So: 2 1 4 − 2 = 2 1 3 + 2 1 2 + ⋯ + 2 1 = 1 6 3 8 4 − 2 = 1 6 3 8 2
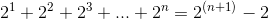
I just grabbed a pen and paper and got stuck in. It was actually a bit of fun that way.