Don't use algebra
A B C D is a square with side length 1 2 , I fold the square and let E ( A ) be on C D .
If F G = 1 5 . What is C E ?
Note: The picture is not drawn to scale.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
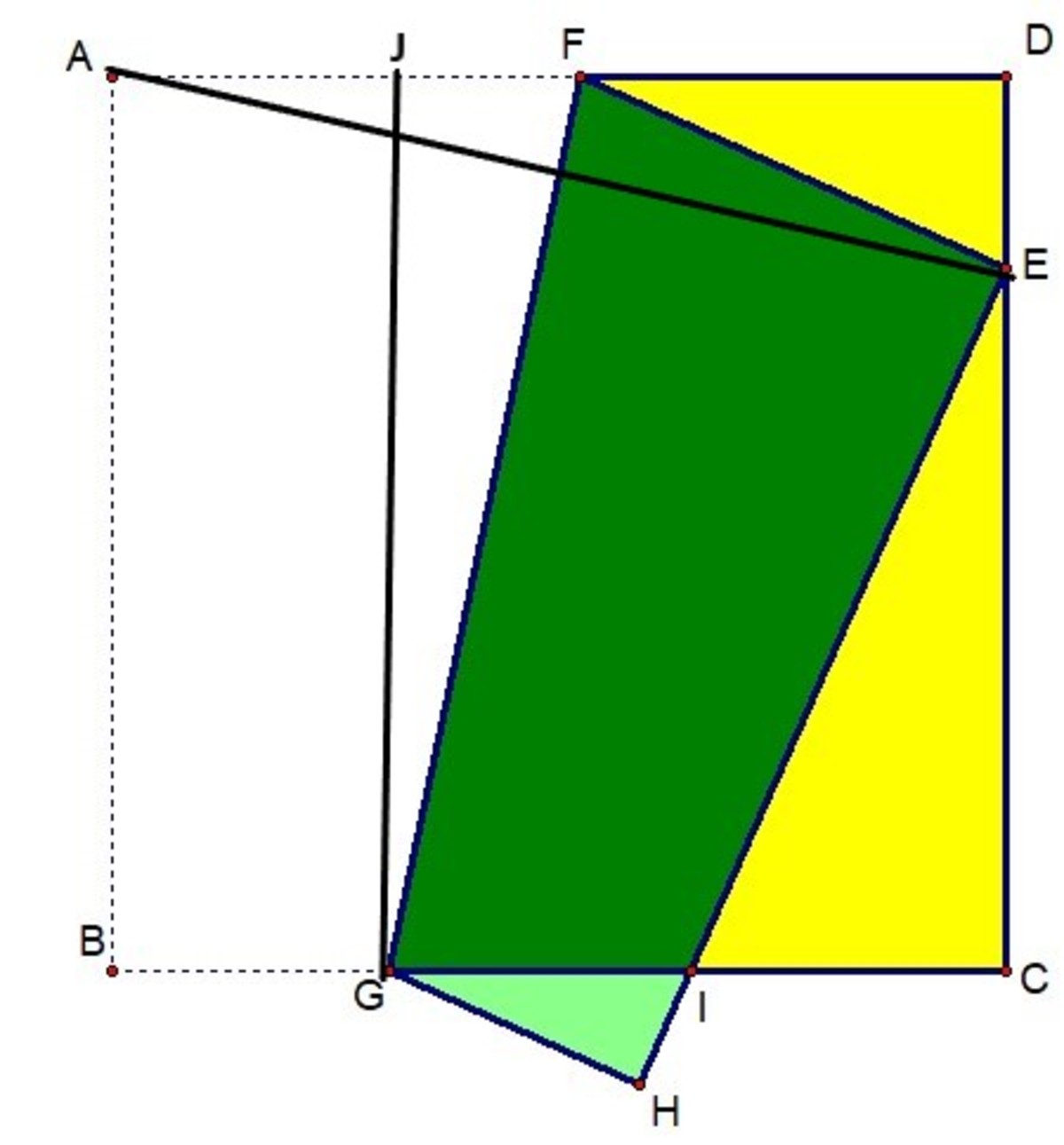 Let
G
J
⊥
A
D
.
G
J
=
A
D
=
1
2
∠
G
J
F
=
∠
A
D
E
=
9
0
∘
∠
D
A
E
=
∠
J
G
F
=
9
0
∘
−
∠
A
F
G
△
G
J
F
≅
△
A
D
E
(
A
S
A
)
So,
G
F
=
A
E
=
1
5
,
D
E
=
1
5
2
−
1
2
2
=
9
,
C
E
=
1
2
−
9
=
3
Let
G
J
⊥
A
D
.
G
J
=
A
D
=
1
2
∠
G
J
F
=
∠
A
D
E
=
9
0
∘
∠
D
A
E
=
∠
J
G
F
=
9
0
∘
−
∠
A
F
G
△
G
J
F
≅
△
A
D
E
(
A
S
A
)
So,
G
F
=
A
E
=
1
5
,
D
E
=
1
5
2
−
1
2
2
=
9
,
C
E
=
1
2
−
9
=
3
We know EF + DF must be 12 as they are one side length of the square. With Phythagoras we know that DE² = EF² - DF². In the right triangle DEF the angle DFE is (through folding) twice as big as the angle BGF - 90°, so angle DEF is 2arccos(12/15)=73.74°. Then we can say that DF = EF*cos(73.74°) = 0.28EF. Now we can solve the equations from the beginning for EF, DF and DE and get EF=9.375, DF=2.625 and DE=9. DE and CE together form one side length of the square so that CE = 12-DE = 3.
A F = F E and ∠ A F G = ∠ G F E ⟹ F G ⊥ A E ∠ n G F = ∠ F A E △ G n F ≅ △ A D E The length of G F = A E = 1 5 , D E = 1 5 2 − 1 2 2 = 9 , C E = 1 2 − 9 = 3