Don't use casual calculus!
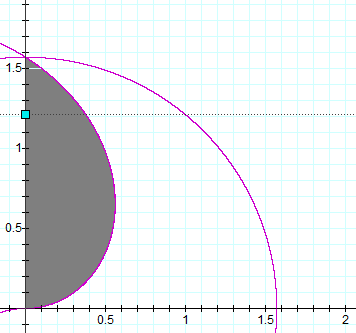 Calculate the shadowed area A int the graph above knowing that the equation for it is
Calculate the shadowed area A int the graph above knowing that the equation for it is
tan ( x 2 + y 2 ) = y / x
Express your answer as ⌈ 1 0 0 0 A ⌉ .
The answer is 646.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Clearly:by the substitution x = r . c o s ( θ ) and y = r . s i n ( θ ) yields : r = θ hence as A is closed area we can write: A = 2 1 ∫ 0 p i / 2 r 2 d r = f r a c p i 3 4 8
This is just an Archimedean spiral, with polar equation r = θ , and the area is A = 2 1 ∫ 0 π / 2 r 2 d θ = 4 8 π 3 ≈ 0 . 6 4 5 9 . The required answer is 6 4 6 .