Don't use trigonometry!

Trig solution (even if it is against the rules)

Law of cosines in $\triangle ABC$ provides: $\cos(CBA)=\frac{12^2+18^2-15^2}{2\times12\times18}=\frac{9}{16}$

Law of cosines in $\triangle BCD$ does the rest: $d^2=12^2+10^2-2\times10\times12\times\cos(CBA)=\boxed{109}$

Using Heron's formula , the area of $\triangle ABC$ is given by:

$\begin{aligned} A & = \sqrt{s(s-a)(s-b)(s-c)} & \small \color{#3D99F6} \text{where }a=12, b=15, c=18, s=\frac {12+15+18}2 = \frac {45}2 \\ & = \sqrt{\frac {45(45-24)(45-30)(45-36)}{2^4}} \\ & = \sqrt{\frac {45(21)(15)(9)}{16}} \\ & = \frac {135\sqrt 7}4 \end{aligned}$

Let the altitude of the triangle $CE$ be $h$ , then $\dfrac {\overline{AB} \times h}2 = A$ $\implies h = \dfrac {135\sqrt 7}4 \times \dfrac 2{18} = \dfrac {15\sqrt 7}4$ .

By Pythagorean theorem , we have $\overline{BE} = \sqrt{\overline{CB} -h^2} = \sqrt{12^2-\left(\frac {15\sqrt 7}4\right)^2} = \dfrac {27}4$ .

$\implies \overline{ED} = \overline{BD} - \overline{BE} = 10 - \dfrac {27}4 = \dfrac {13}4$ and by Pythagorean theorem again:

$\begin{aligned} d & = \sqrt{h^2+ \overline{ED}^2} = \sqrt{\left(\frac {15\sqrt 7}4\right)^2 - \left(\frac {13}4\right)^2} = \sqrt{109} \end{aligned}$

$\implies d^2 = 109$

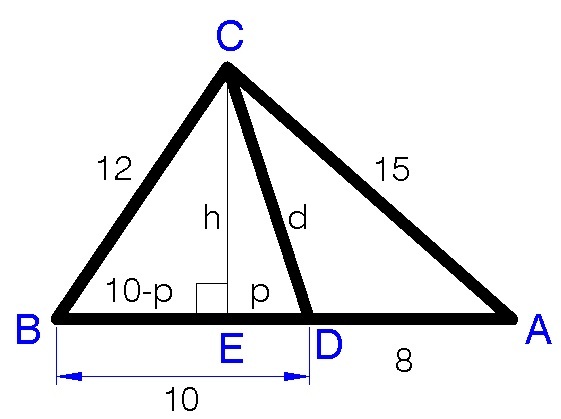Draw the altitude $CE=h$ . Let $ED=p$ .

Considering triangle CBD:

Applying Pythagorean Theorem at $\triangle CEB$ , we have

$12^2=h^2+(10-p)^2$

$144=h^2+(100-20p+p^2)$

$144=h^2+100-20p+p^2$

$44=h^2-20p+p^2$ $\color{#D61F06}(1)$

Applying Pythagorean Theorem at $\triangle CED$ , we have

$d^2=p^2+h^2$ $\implies$ $h^2=d^2-p^2$

Replacing $h^2$ in $\color{#D61F06}(1)$ , we obtain

$44=d^2-p^2-20p+p^2$

$d^2=44+20p$ $\color{#D61F06}(2)$

Considering triangle CDA:

Applying Pythagorean Theorem at $\triangle CEA$ , we have

$15^2=h^2+(8+p)^2$

$225=h^2+(64+16p+p^2)$

$225=h^2+64+16p+p^2$

$161=h^2+16p+p^2$ $\color{#D61F06}(3)$

But $h^2=d^2-p^2$

Substitute $h^2$ in $\color{#D61F06}(3)$ ,

$161=d^2-p^2+16p+p^2$

$161=d^2+16p$

$d^2=161-16p$ $\color{#D61F06}(4)$

Equate $\color{#D61F06}(2)$ and $\color{#D61F06}(4)$ :

$d^2=d^2$

$44+20p=161-16p$

$36p=161-44$

$36p=117$

$p=\dfrac{117}{36}$

Then, solve for $d$ by substituting $\dfrac{117}{36}$ for $p$ in $\color{#D61F06}(2)$ or $\color{#D61F06}(4)$

$d^2=161-16p$

$d^2=161-16(\dfrac{117}{36})$

$d^2=109$

$d=\sqrt{109}$

Finally,

$d^2 = 109$

$Let~X=BE.\\ Using~Pythagorean~ theorem, ~in~\Delta s, ~CBE~and~CEA,\\ 12^2~-~X^2=h^2=15^2~-~(18 - X)^2.\\ \therefore~81-18^2+36X=0.~~\implies~X=\dfrac {27}4.\\ So~~~d^2=h^2+X^2=(12^2 - X^2)+(10-X)^2\\ =144-20*X+100=\large \color{#D61F06}{109}.$