Don't Waste Too Much Time!

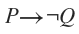
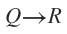
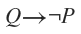
This question relies on not making any assumptions, and a careful reading of the conditions. Here's an explanation of each of the options:

1. "If Jeff spends 5 hours playing video games, then he will fail his next math test." - False, while he will not finish his math homework, it is never mentioned that not finishing it will lead to failure in his next math test.
2. "If Jeff does not finish his math homework, then he spent 5 hours playing video games." - False, he could have spent a different amount of time playing video games and still have decided not to do his math homework.
3. "If Jeff does well on his next math test, then he finished his math homework." - False, the math homework guarantees his success but he can still do well even if he doesn't do it.
4. "If Jeff does not finish his math homework, then he does not do well on his next math test." - False, same reason as 3.
5. "If Jeff does not play video games, then he will do well on his next math test." - False, he may do well but his success is not guaranteed unless he does his math homework.
6. "If Jeff finishes his math homework, then he did not spend 5 hours playing video games." - True, it is mentioned that he cannot finish the homework if he spends 5 hours playing video games, so he must not have.
7. "If Jeff spends 2 hours playing video games, then he can finish his math homework." - False, the conditions never mention when he can finish the homework, so we can't assume that 3 more hours is sufficient.
8. "If Jeff does not fail his next math test, then he did not spend 5 hours playing video games." - False, it's also possible for him to succeed if he plays for 5 hours.

So the correct option is: "If Jeff finishes his math homework, then he did not spend 5 hours playing video games."

This question can be solved using the proportional calculus. Here are the two statements given:

Statement #1 : "If Jeff spends 5 hours playing video games, then he cannot finish his math homework".

Statement #2 : "If Jeff finishes his math homework, then he will do well on his next math test".

Let

• P = "Jeff spends 5 hours playing video games"
• Q = "Jeff finishes his math homework"
• R = "Jeff will do well on his next math test"

So

Statement #1 can be written as (P implies negation Q) and

Statement #2 can be written as (Q implies R)

A conditional statement is always logically equivalent to its contrapositive. So, among the given options the only reasonable choice is

"If Jeff finishes his math homework, then he did not spend 5 hours playing video games." i.e. which is contrapositive of statement #1.

"If Jeff finishes his math homework, then he did not spend 5 hours playing video games" is the only option which must be true.