Breaking A Trapezium Apart
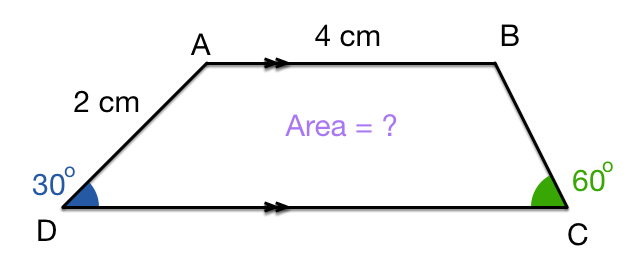
In the figure above, is parallel to . If and , angles and are and respectively. Find the area of the figure (in ).
Give your answer to 3 decimal places.
The answer is 5.155.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A B C D has 4 sides, it is a quadrilateral. Two of its sides are A B and C D are parallel. Therefore, A B C D is a trapezium/trapezoid.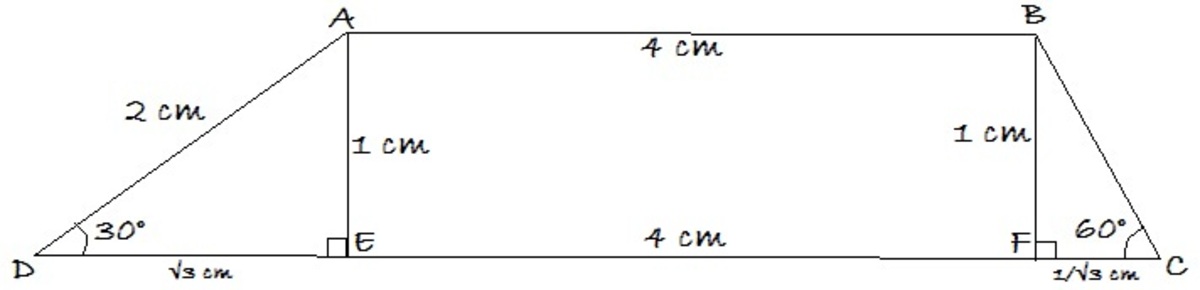
We drop perpendiculars to C D i.e. A E ⊥ B C and B F ⊥ B C . E and F are points on side C D . Then in triangle A E D ,
cos 3 0 ∘ = A D E D = 2 E D ⇒ 2 3 = 2 E D ⇒ E D = 3 cm .
By Pythagorean theorem , A E = 1 cm . Clearly A E ⊥ B F (Perpendicular distances between parallel lines are equal).
Then B F = 1 cm . Following to this, in triangle B F C ,
tan 6 0 ∘ = F C B F = F C 1 ⇒ 3 = F C 1 ⇒ F C = 3 1 cm .
Now, C D = E D + F E + F C = 3 + 4 + 3 1 .
Area of a trapezium/trapezoid is
2 1 × ( sum of parallel sides ) × ( height ) = 2 1 ( A B + C D ) × 1 = 2 1 ( 4 + 3 + 4 + 3 1 ) .
Solving it and evaluating it correct to 3 decimal places, we get 5 . 1 5 5 as the answer.