Dot Expansion

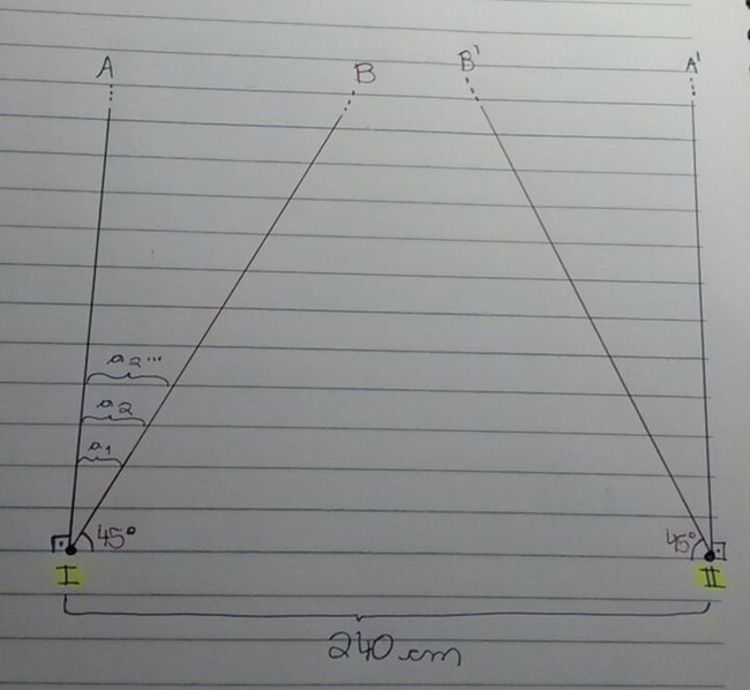There are two equal dots, I and II. Both dots are in the same horizontal line, called C, at a distance of 240cm from each other. The dot I expands itself, creating an infinite line, called A, which makes 90 degrees with C. The dot II does the same, but the line created is called A'. The dot I also expands itself to the right, creating another line, called B, that makes a 45 degrees angle with C. At the same time, the dot II starts to expand itself to the left, creating a line, called B', that also makes a 45 degrees angle with C. Dot I expands the line B by 1,2cm each second, and so does dot II to the line B' (their speed on the lines B and B' is $v = 1,2 \text{ cm/s}$ ) . Let $\alpha$ be the time, in seconds, that it takes to both dots meet in their expansions on the lines B and B'. Also, let $\beta$ be the distance, in centimeters, that the dot II runs on the line B' until it meets the dot I on the line B. Consider $\epsilon = \alpha + \beta$ . What is the value of $\lfloor\epsilon\rfloor$ ?

Notes and Assumptions :

Use a protractor on a notebook page to create the lines B and B'. Try to do just as the image. Do not use trigonometric measures for the given angles (for real). Also, consider that the initial positions, vertical and horizontal, of both dots is 0 centimeters.