Dots And Hexagons

Logic Level 5

Consider the image below:

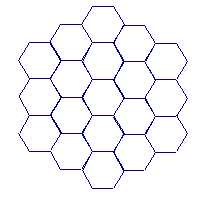
Imagine you were playing a two-player game that involves each player taking turns draw a dot on one of the vertices of this graph. The rules for where a player can draw a dot are as follows:

A player can only draw a dot on a vertex that has not already been drawn on.
A player cannot draw a dot adjacent to another dot.

The game ends when a player is unable to place another dot. What is the minimum number of dots that can be placed in one complete game?

Bonus: can you generalize this for all other centered hexagonal boards?

Inspired by Settlers of Catan

The answer is 15.

2 solutions

Garrett Clarke
Aug 27, 2015

Here's my solution!

I don't know if it's unique or not; maybe someone else has another solution! I hope so!

All vertices have either 2 or 3 neighbours.

There are 18 vertices with 2 neighbours and 36 vertices with 3 neighbours. There are 54 vertices in total.

You can cover 3 or 4 vertices by placing a dot.

So, the no. of dots required cannot be less than $\left\lceil \frac { 54 }{ 4 } \right\rceil = 14$

With this, we know that the answer cannot be less than 14.

I am not sure how to prove 14 is impossible though, i have the idea that we somehow are forced to place more than 2 dots on vertices with 2 neighbours or vertices with 3 neighbours but at least 1 of the neighbour being shared.

If this can be proven, then 15 will be the next minimum and you have prove its existence.

By the way, the solution is not unique, you can perform many ways of rotations and reflection to get different arrangement.

Lam Yet Sin - 5 years, 7 months ago

There are 28 solutions with 15 settlements. I am counting rotations and reflections as different, but not all of them are rotations and reflections of each other. Drive permanent marker stakes numbered 0-53 into each intersection in Catan. If two solutions cover the same set of markers, they are the same.

Consider the 6 intersections around the center hex. You can have 5 classes of arrangement of these: 0 settlements (1 rotation), 1 settlement (6 rotations), 2 settlements 2 apart (6 rotations), 2 settlements 3 apart (3 rotations), and 3 settlements 2 apart (2 rotations). You cannot rotate a member of one class and get a result of a different class. For 15 settlements, there are: 12 solutions with 2 settlements 2 apart, 12 solutions with 2 settlements 3 apart, and 4 solutions with 3 settlements 3 apart around the center hex. As it happens, there are no solutions for 15 settlements with 0 or 1 settlements around the center hex, but there are for 16 settlements.

There are 2 solutions with 27 settlements (the maximum number you can fit). These are a rotation of each other. The way I numbered the intersections (essentially an outward clockwise spiral), one solution puts settlements at all even-numbered intersections, and the other at all odd-numbered intersections.

There are about 1.4 million solutions for 15-27 settlements, the range of what's possible.

Gordon Burditt - 1 year, 9 months ago

This is awesome, thanks for the analysis! If you can, link your code, I'd be interested in taking a look at it.

Garrett Clarke - 1 year, 6 months ago

The vertices lie on 3 concentric "rings".

There are 18 vertices that lie on the outside ring and do not share an edge with a vertex from the middle ring. There are 6 vertices that lie on the middle ring and share en edge with a vertex from the inner ring.

Notice that taking any group of one vertex and its neighbors can not contain both types of vertices, can contain at most 2 vertices of the first type, and at most one vertex of the second type.

This implies you need at least 18/2+6=15 vertices to cover them all.

The logic of these critical groups of vertices can be generalized for a larger board.

Eilon Lavi - 4 years, 5 months ago

You can generalize for a larger board, but doing so doesn't seem to improve the solution. Extending to include hexes of distance 3 or more results in lower bounds for the minimum number of settlements below the bound given by ceil(n/4) where n is the total number of intersections. The approach produces an improved minimum for a distance-2 map, and equally-as-good results for a distance-0 and distance-1 map, and worse minimums for distance-3 and above (well, I only tested to distance-17).

I number rings starting with Ring 0 as the boundary of the center hex, and increasing as you go outward. The Catan base game board is a "distance-2" map and has rings 0, 1, and 2. Split each ring into two sub-rings: vertices in ring r with a neighbor in ring r-1 are in the inner sub-ring. Vertices in ring r with a neighbor in ring r+1 are in the outer sub-ring. Ring 0 has no inner sub-ring: all of the vertices in ring 0 have neighbors in ring 1, and there is no ring -1.

Consider a group of any three adjacent sub-rings. The middle sub-ring must be in the map. The inner or outer sub-ring (or in the case of a distance 0 map consisting only of the center hex, both) may be outside the map. (Logical places to start for the middle ring are the outer ring 0 sub-ring, the inner ring 1 sub-ring, and the outer ring 1 sub-ring).Any vertex in any of the 3 sub-rings, plus its neighbors, includes a vertex in the middle sub-ring. All of the vertices in the middle sub-ring have no neighbors outside the group of 3 sub-rings.

Now make more groups of 3 sub-rings to include the whole map, and possibly sub-rings outside the map but adjacent to the map. If you end up with the outer sub-ring of the outermost ring left over, the only conclusion is that you need at most 0 vertices to cover them (they could be covered by the inner sub-ring of the same ring). A vertex and its neighbors contain one or more vertices from at most one middle ring of a group.

If the middle ring is the outer sub-ring of ring 0, one vertex and its neighbors in that group can cover at most 3 vertices in the middle ring. If the middle ring is the inner sub-ring of ring 1, one vertex and its neighbors in that group can cover at most 1 vertex in the middle ring. If the middle ring is the outer sub-ring of ring 1, or any sub-ring of a ring >= 2, one vertex and its neighbors in that group can cover at most 2 vertices in the middle ring.

For a distance 3 map, starting with the first middle ring as the outer ring 0 sub-ring, you need at least 6/3 + 12/2 + 24/2 = 20 vertices. Starting with the first middle ring as the inner ring 1 sub-ring, you need 6/1 + 18/2 = 15. Starting with the first middle ring as the outer ring 1 sub-ring, you need 12/2 + 18/2 = 15. Take the highest one, 20. Note that all of these are less than 24, determined by the ceil(96/4) formula. I don't know whether there is a solution for 24 or 25, but I have a solution for 26.

The Catan map for 5-6 players is sorta halfway between a distance-2 and a distance-3 map. It looks like an irregular hexagon with 2 pairs of 4-on-a-side hexes and 1 pair of 3-on-a-side hexes. It doesn't have all the symmetries of a distance-N map and has an incomplete outer ring. I do not know whether there is a solution for 20, but I have a solution for 21.

For a distance 7 map, starting with the first middle ring as the outer ring 1 sub-ring, you need at least 12/2 + 18/2 + 30/2 + 36/2 + 48/2 = 72, but the ceil(n/4) formula gives 96.

How do I go about posting images on this forum? Solutions are best shown as images.

Gordon Burditt - 1 year, 5 months ago

Joe Mansley
Sep 2, 2020

There are multiple ways to do it with 15 dots. I will show that 14 dots is not sufficient.

Let's say that a dot 'covers' a vertex if it's the first dot placed either on or adjacent to that vertex. Each dot covers at most 4 vertices. If 3 or more cover fewer than 4 vertices then the number of vertices covered $\leq 14*4-3=53 < 54$ , so the game can't be completed.

Look at the top picture in the question. Consider the top row of 3 hexes. (6,5,3 or forest, field, mountain.) Number the vertices on the top of this row 1,2...7 (with 1,2,3 on the forest, 3,4,5 on the wheat etc).
Suppose every dot on this row covers 4 vertices. Then there can be no dots on vertices 1,2,4,6,7 (since then they couldn't cover 4 vertices). But vertices 2 and 6 must be covered. So there must be dots on vertices 3 and 5. But they can't both cover vertex 4. Thus there must be a dot on this row covering <4 vertices.

Rotate $2\pi/3$ radians and do the same with another row, and then once more, and we find there must be 3 dots covering <4 vertices. (The 3 dots are distinct since the 3 rows don't overlap.)

Thus the game cannot be completed with only 14 dots.

Dots And Hexagons

Inspired by Settlers of Catan

The answer is 15.

2 solutions

0 pending reports