Dotted?

$\begin{aligned} \alpha & = \int_0^1 x {\color{#3D99F6} \cos (\cos (\cos (\cdots x) ) )} \ dx & \small \color{#3D99F6} \text{Let }y = \cos (\cos (\cos (\cdots x))) \\ & \approx \int_0^1 {\color{#3D99F6} 0.73909}x \ dx & \small \color{#3D99F6} \implies y = \cos y \approx 0.73909 \\ & = \frac {0.73909 x^2}2\ \bigg|_0^1 \\ & = 0.369545 \end{aligned}$

Therefore, $\lfloor 10^3 \alpha \rfloor = \boxed {369}$ .

First step is to write an equation for the nested function. To do this we will set up the equation:

$x\cos { (\cos { (\cos { (...x) } ) } ) } =y$

Then we can manipulate the equation to get:

$\cos { (\cos { (\cos { (...x) } ) } ) } =\frac { y }{ x }$

Notice that the nested cosines inside of the first cosine equals $\frac { y }{ x }$ . So we can substitute the nested cosines for $\frac { y }{ x }$ . So the equation becomes

$\cos { \frac { y }{ x } } =\frac { y }{ x }$

When we graph this equation in desmos it looks like this:

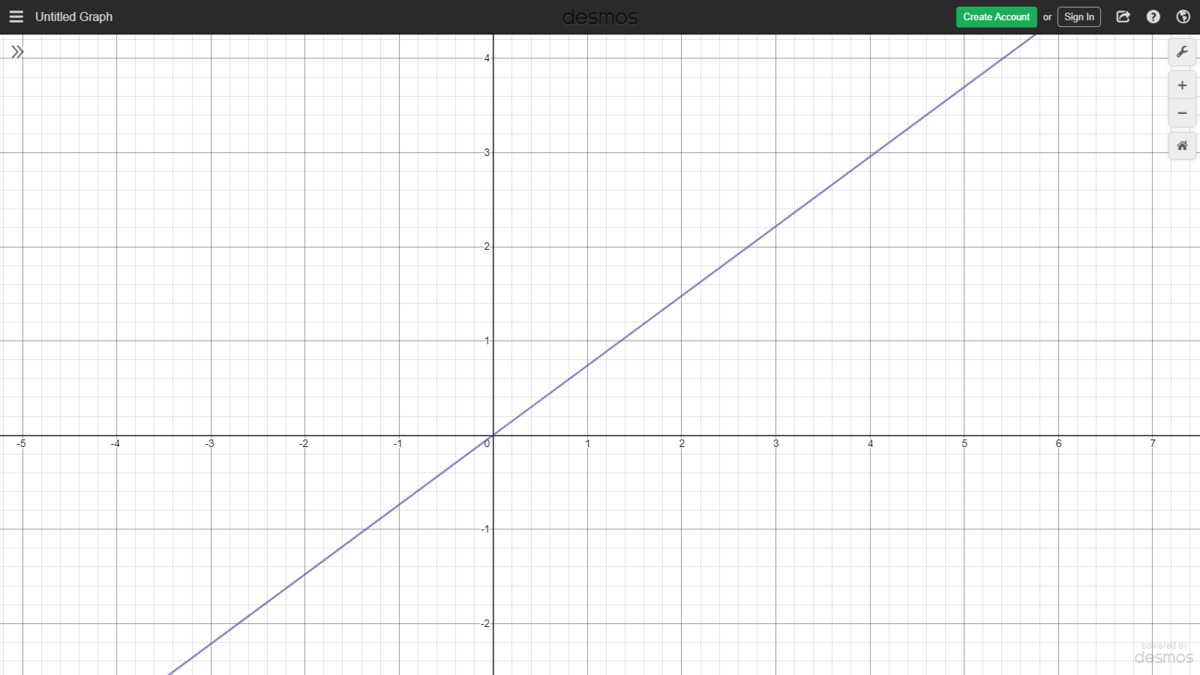
Notice that the graph is a straight line. To approximate the slope of the equation, we can zoom into the graph when $x=1$ and find the value of $y$ at that point. When we do this, we find that the slope of the line is approximately $0.739085$ .

This means that $\int _{ 0 }^{ 1 }{ 0.739085x } dx \approx \int _{ 0 }^{ 1 }{ x\cos { (\cos { (\cos { (...x))) } } } }$ . When we evaluate the integral we get that $a\approx \int _{ 0 }^{ 1 }{ 0.739085x } =0.3695425$

When we plug the value of $a$ into $\left\lfloor { 10 }^{ 3 }a \right\rfloor$ , we get 369.

So our answer is 369 .

Note:

In my original answer, I graphed the function inside of the integral in desmos to prove that it was a linear function and find its slope. However, we can prove that the function is linear in a more formal and maybe better way. In the original answer, we found that the function that was equivalent to the function inside of the integral was:

$\cos { \frac { y }{ x } } =\frac { y }{ x }$

We can substitute $\frac { y }{ x }$ for $u$ .

The equation becomes $\cos { (u)=u }$ .

When we do this we realize that the value of $u$ is the Dottie Number .

This means that $u=\frac { y }{ x } \approx 0.739085$ .

Notice that $\frac { y }{ x }$ is constant meaning that the function inside of the integral is a linear function with a y-intercept of $0$ and an approximate slope of $0.739085$ . So the integral becomes $\int _{ 0 }^{ 1 }{ 0.739085x } dx$ . When we evaluate this integral and plug it in into $\left\lfloor { 10 }^{ 3 }a \right\rfloor$ , we get 369.

This is not a proof. I note the following $\int_0^1 x \, dx \Rightarrow \frac12$ . And, that $\int_0^1 x \cos (\cos (...(\cos (\cos (x))))) \, dx$ appears to limit as the number of cosine functions goes to $\infty$ to the Dottie number which appears to be double the answer to this problem. The Dottie number does not appear to have a closed form.

$\left[x\right]$ usually means round to closest integer, with some ambiguity of how to handle $\frac12$ : always greater magnitude, always lesser magnitude, towards $+\infty$ , towards $-\infty$ , to the adjacent even or odd integer, etc.

$\lfloor x\rfloor$ usually means the floor function.