Double Bubble Gum
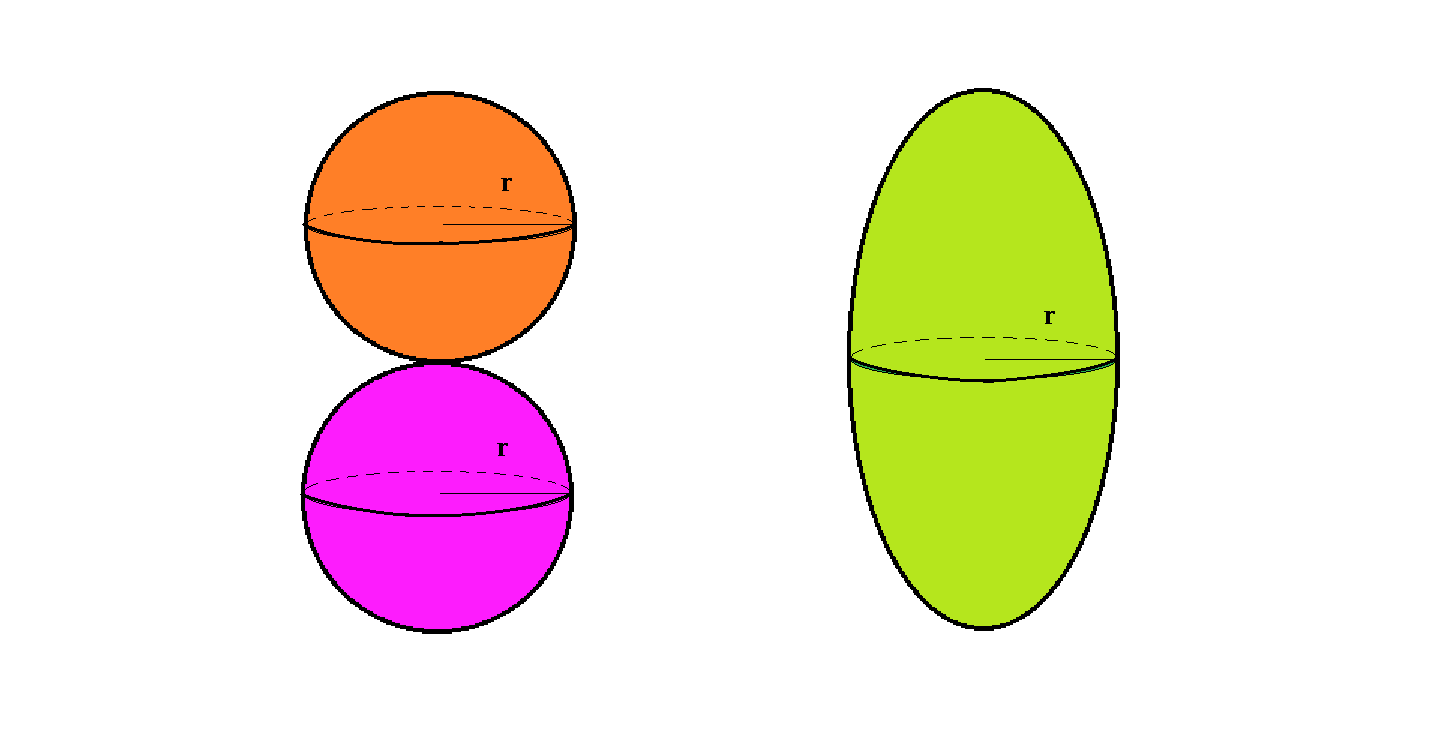
A bubble gum shop sells its products in 2 different styles: a spherical ball and an elliptical gum, as illustrated in the images above.
The innovative elliptical gum has its minor axis equal to the radius of the ball, while its height is twice that of the ball.
If you were to choose between 2 gum balls and 1 elliptical gum, which option would give you more gum?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Volume of Revolution - Disc Method - Intermediate
Let R be the radius of the sphere. Then the oval will have its minor and major axis equal to R and 2 R respectively.
By drawing an elliptical graph of the oval, we can then come up with the equation with center on the origin:
R 2 x 2 + ( 2 R ) 2 y 2 = 1
x 2 = R 2 − 4 y 2
By revolving the graph around the y-axis, we can calculate volume V of half the oval as:
V = ∫ 0 2 R ( π x 2 ) d y = ∫ 0 2 R π ( R 2 − 4 y 2 ) d y = π [ R 2 y − 1 2 y 3 ∣ 0 2 R ] = π [ 2 R 3 − 1 2 8 R 3 ] = π R 3 ( 2 − 3 2 ) = 3 4 π R 3
Clearly, this is a formula for the sphere with radius R .
In other words, half an oval has the same volume as one sphere.
Thus, the volume of 2 spheres = the volume of 1 oval.
Both options would give the same volume of gum.