Double collision in projectile
A ball is projected from a point in a horizontal plane so as to strike a vertical wall at right angle at point A after rebounding from the wall it strikes the horizontal plane once and returns to the point of projection just before second collision at horizontal surface. Find the coefficient of restitution for the two collisions, assuming it to be same for both the collision .
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
such a long Solution :P mains ki prrep hogi ?
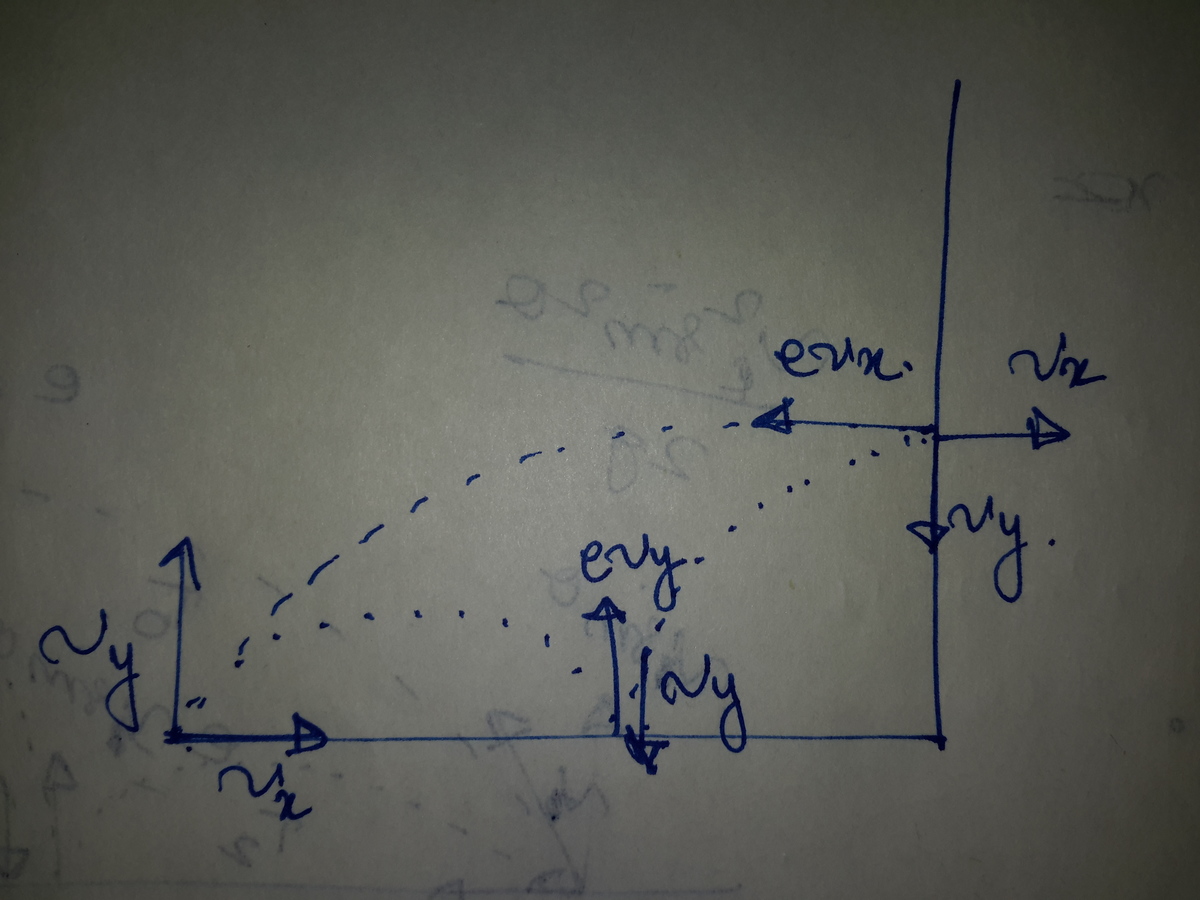
Total ascend distance,
s = g v x ⋅ v y
After collision 1,
v 1 − x = e ⋅ v x , v 1 − y = v y
t 1 = g v y
⇒ s 1 = v 1 − x ⋅ t 1 = g e ⋅ v x ⋅ v y
After collision 2,
v 2 − x = e ⋅ v x , v 2 − y = e ⋅ v y
t 2 = g e ⋅ v y
⇒ s 2 = v 2 − x ⋅ t 2 = g e ⋅ v x ⋅ e ⋅ v y
Now,
s = s 1 + s 2
⇒ g v x ⋅ v y = g e ⋅ v x ⋅ v y + g e ⋅ v x ⋅ e ⋅ v y
Simplifying, 2 e 2 + e − 1 = 0
Or, e = 4 − 1 ± 1 + 8 = 4 2
∴ e = 0 . 5
In step 3 from where u get the coefficient of e^2
Note: I have used some terms in the solution which i am defining
x = initial angle of projection
u = initial velocity of projection
e = coefficient of restitution
R= Horizontal Range of projectile thrown initially
Lets Consider That We Have Thrown The Ball With An Initial Velocity u at an
angle x with the horizontal.
Now The Important point to be noted is that if it strikes the VERTICAL WALL
PERPENDICULARLY then it must be moving horizontally at that particular
moment . Hence The collision MUST TAKE PLACE AT HIGHEST POINT .
As We know
at the topmost point of trajectory the particle only has horizontal component of
velocity as it does not change throughout the flight .
Lets Suppose the coefficient of restitution at the pair of surfaces is e
After the collision with wall it will rebound with a velocity eucosx
Now this will become the case of horizontal projection from a height .
we can find out the velocity with which the projectile will strike the ground first
time .
We can Apply Third equation of kinematics to see that(In vertical direction)
v = usinx
Also we can find out the horizontal distance covered by particle using second
equation of kinematics
x=eR/2 1.....
Velocity in horizontal direction will remain same as eucosx .
Now when the ball will collide the with the floor the line of impact will be
vertical . so the ball will rebound with a velocity eusinx in vertical direction and
velocity eucosx will remain unchanged as it will be perpendicular to the line of
impact .
It will be a case of normal projectile on ground.
It is easy to see that that projectile will now start at an angle x with the
horizontal .
Applying formula of range of projectile
y = R*e^2 2.........
In Order to reach the point of projection
The total Horizontal distance to be covered by the particle = R/2
Hence
1......+ 2....... = R/2
Solving the about equation
We get a quadratic in e
e = -1 or 0.5
Neglecting Negative value
e= 0.5 Nice Problem!