Double Gamble

Probability Level 1

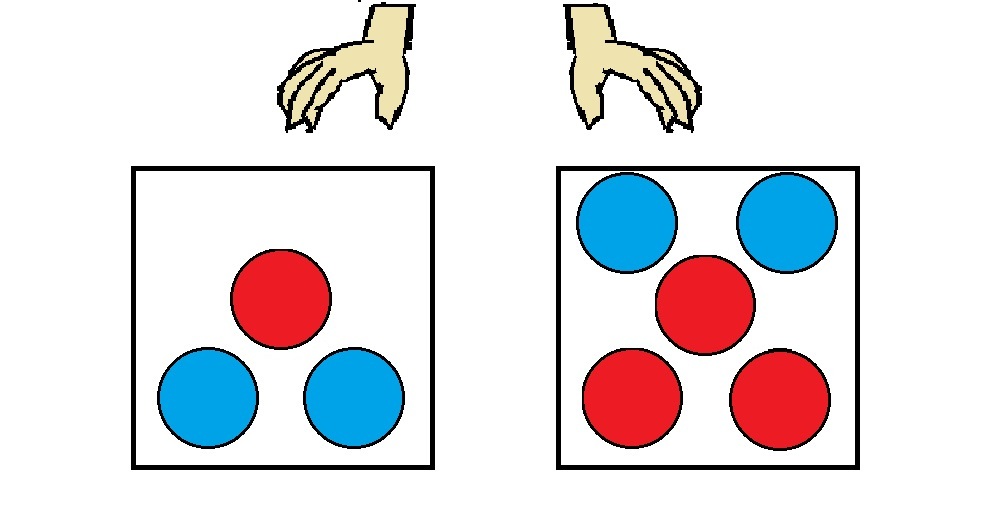
As shown above, the left box contains 1 red ball and 2 blue balls while the right box contains 2 blue balls and 3 red balls.

In a lucky draw game, you have to randomly and simultaneously pick up one ball from each box using both hands.

If you get a blue ball from the left box, you'll be rewarded 4 dollars, but you'll lose 5 dollars for the red draw. On the other hand, a red ball drawn from the right box will cost you 7 dollars while a blue draw will earn you 8 dollars.

What is the expected value of the bet earned from this game?

The answer is 0.

1 solution

Worranat Pakornrat
May 20, 2016

Relevant wiki: Expected Value

The expected value = $\sum P_{i}E_{i}$ , where $P$ is the probability of an event and $E$ is the event of earning.

Since the draws from both boxes are independent from each other, we can simply add up the expected values from both scenarios.

Therefore, the expected value = $\dfrac{2}{3}\times 4 + \dfrac{1}{3}\times (-5) + \dfrac{3}{5}\times (-7) + \dfrac{2}{5}\times 8 = \dfrac{8-5}{3} + \dfrac{16-21}{5} = 0$ .

Hence, the expected gain of this bet is $\boxed{0}$ dollars.

Moderator note:

Good simple explanation.

In general, it is best to avoid an answer of 0, unless you want to stress a certain property.

Double Gamble

The answer is 0.

1 solution

Moderator note:

0 pending reports