Double Integral 2

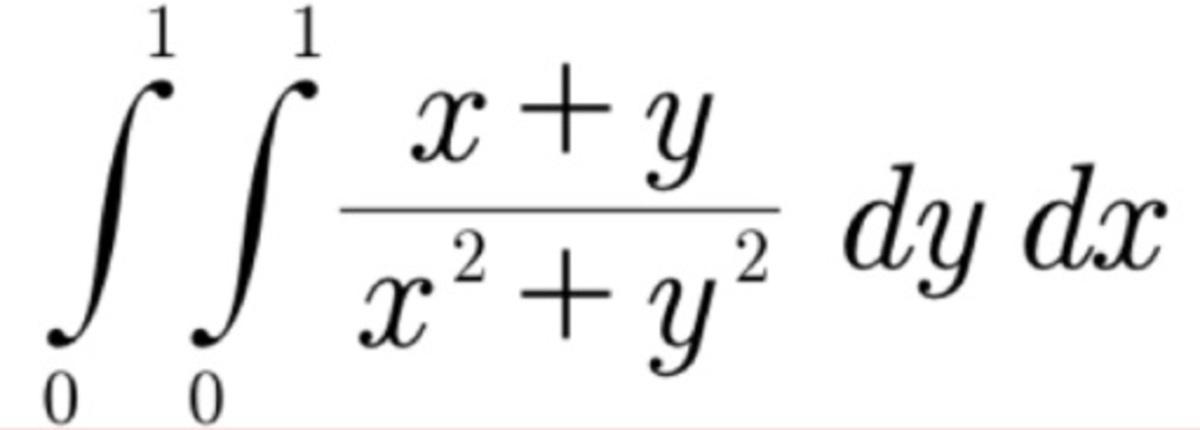
The integral is evaluated over a unit square henceforth referred to as the region $D$ , one of the vertices of which is the origin. Converting this integral to polar coordinates:

$x = r \cos{\theta}$ $y = r \sin{\theta}$

The area element in polar coordinates is:

$dA = r \ dr \ d\theta$

Applying these substitutions, the integrand simplifies to:

$\frac{\cos{\theta}+\sin{\theta}}{r}$

The right side of the square has the equation in polar coordinates (as $\theta$ varies from $0$ to $\pi/4$ ):

$r = \sec{\theta}$

The top side of the square has the equation in polar coordinates (as $\theta$ varies from $\pi/4$ to $\pi/2$ ):

$r = \cosec{\theta}$

The integral simplifies to:

$I = \int_{0}^{1} \int_{0}^{1} \frac{x+y}{x^2+y^2} \ dy \ dx = \int \int_{D} \frac{\cos{\theta}+\sin{\theta}}{r} \ r \ dr \ d\theta$ $\implies I = \int \int_{D} (\cos{\theta}+\sin{\theta}) \ dr \ d\theta$

$I = \int_{0}^{\pi/4} \int_{0}^{\sec{\theta}} (\cos{\theta}+\sin{\theta}) \ dr \ d\theta +\int_{\pi/4}^{\pi/2} \int_{0}^{\cosec{\theta}} (\cos{\theta}+\sin{\theta}) \ dr \ d\theta$ ]

$\implies I = \int_{0}^{\pi/4} (1+\tan{\theta}) \ d\theta + \int_{\pi/4}^{\pi/2} (1+\cot{\theta}) \ d\theta$

for the second integral on the RHS, substitute $\phi = \pi/2 - \theta$ and the resulting integral transforms to (after simplification):

$I =2 \int_{0}^{\pi/4} (1+\tan{\theta}) \ d\theta$

Evaluating:

$\boxed{I = \frac{\pi}{2} + \ln{2}}$

We integrate first with respect to $y$ to obtain the following integral

$\dfrac{1}{2}\displaystyle \int_0^1 \ln \left (\frac{x^2+1}{x^2}\right ) dx+\displaystyle \int_0^1 \cot^{-1} (x)dx$ .

Integrating these, we finally obtain the value of the given integral as

$\dfrac {2\ln 2+π}{2}\approx \boxed {2.2639}$ .