Double Oscillator
A massive point particle is attached to the end of a massless, rigid rod of length L . The other end of the rod is attached to a hinge which moves up and down sinusoidally: y h = A sin ( ω t ) . There is an ambient downward gravity, and at time t = t 0 , the rod initially makes an angle of θ 0 with the vertical.
What is the maximum value of θ (in degrees) as the system evolves over time?
Details and Assumptions:
- g = 1 0 m/s 2 .
- L = 1 m .
- A = 0 . 2 5 m .
- f = 1 0 0 Hz , ω = 2 π f = T 2 π .
- t 0 = 2 T .
- θ 0 = 5 ∘ , θ ˙ 0 = 0 .
- If you believe that the oscillation in θ is not periodic, give the maximum θ value in the time range ( t 0 , t 0 + 1 0 0 T ) .
The answer is 12.547.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Thanks for the solution. What simulation time step did you use?
I believe you made a typo in writing out expression for kinetic energy, it should be T = 2 1 m ( ( L θ ˙ cos θ ) 2 + ( A ω cos ω t − L θ ˙ sin θ ) 2 ) .
You're right. I've corrected the error.
In an accelerating frame of reference, that moves together with the oscillating hinge, the effective acceleration of gravity is g − A ω 2 sin ( ω t − ϕ 0 ] , where ϕ 0 = ω t 0 = π . The equation of motion is similar to a simple pendulum, except this time we use the effective acceleration of gravity:
Θ ¨ = [ g − A ω 2 sin ( ω t − ϕ 0 ] sin Θ / L
Numerical integration yields to following plot of the angle vs. time:
The motion seems to be quasi-periodic, and the maximum deviation can be seen as 12.45 ∘ . In the parameter range specified here the acceleration of gravity barely plays a role, because g < < a ω 2 . It is interesting to note that for ϕ 0 = − π / 2 the maximum angle is equal to the initial angle.
This type of "inverted pendulum" has been first studied in great detail by the Nobel Laureate Pytr Kapitza in the former Soviet Union. For A < < L (not the case here) and ω > > g / l the motion can be separated into a slow and a fast component, and there is an analytical solution. The evolution of the slow component is determined by an effective potential that depends on the oscillation of the hinge.
Greetings. Do you suppose it is genuinely periodic, or only approximately periodic? I figured it was periodic, but didn't have a proof, since I used numerical integration to solve. I suppose this problem is analogous to the standard pendulum, in that nice analytical solutions may only exist for small values of A.
Log in to reply
I do not think that the motion is strictly periodic. There is a large literature on this problem, and for the most general case the motion is chaotic. This happens especially if the driving frequency is close to the natural frequency of the pendulum.
Analytical solution indeed exists for small A, if the driving frequency is much larger than the natural frequency of the pendulum. The motion can be separated to slow and fast components. The slow component has a relatively simple motion in an effective potential. This is nicely discussed in https://en.wikipedia.org/wiki/Kapitza%27s_pendulum . In the small A limit the initial angle will be the largest angle, just as in the case of regular pendulum.
Another interesting case is when the initial angle is small, and we can replace sin θ with θ in the equation of motion. The equation of motion becomes a Mathieu differential equation, http://mathworld.wolfram.com/MathieuFunction.html . The solutions are the (surprise!) Mathieu functions. Interestingly, we know that for certain discrete values of the parameters the solution is periodic; otherwise it is not.
Plotting the maximum oscillation amplitude as a function of A, one gets the following results:
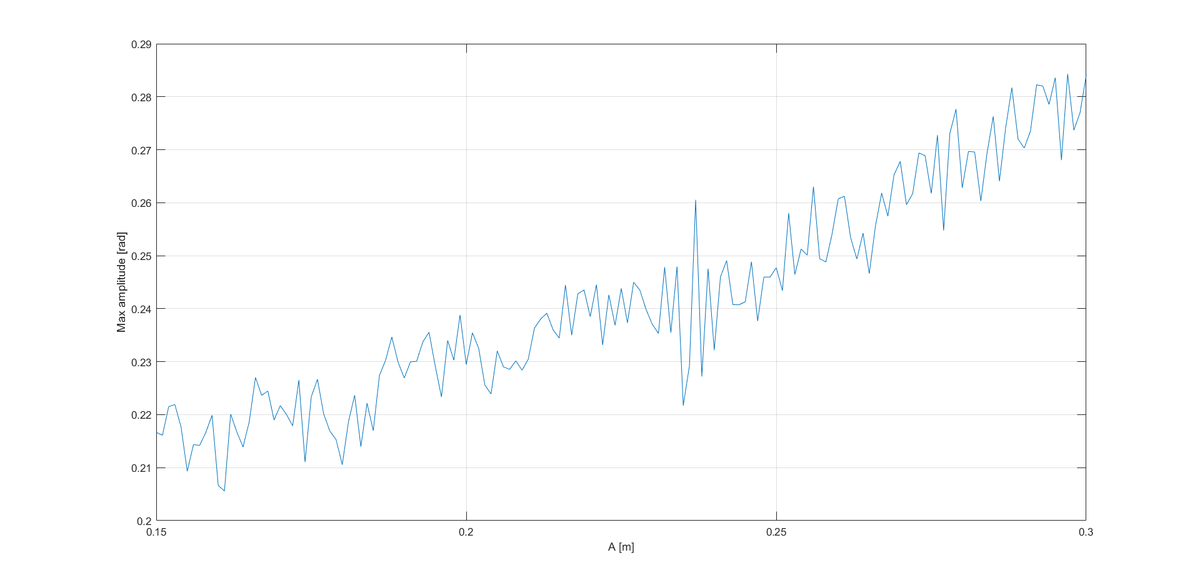
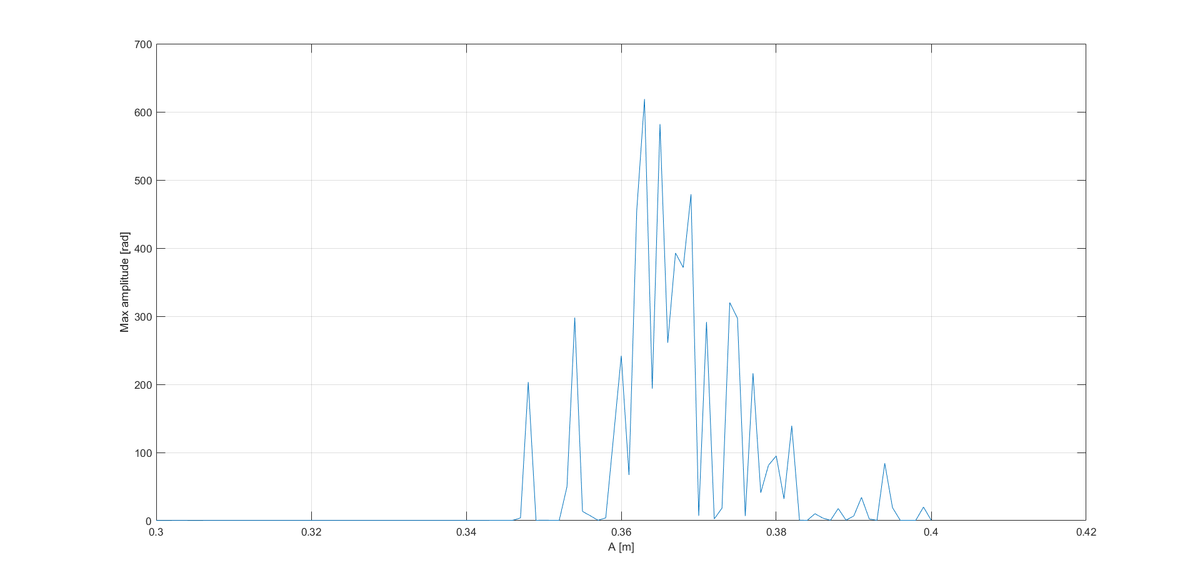
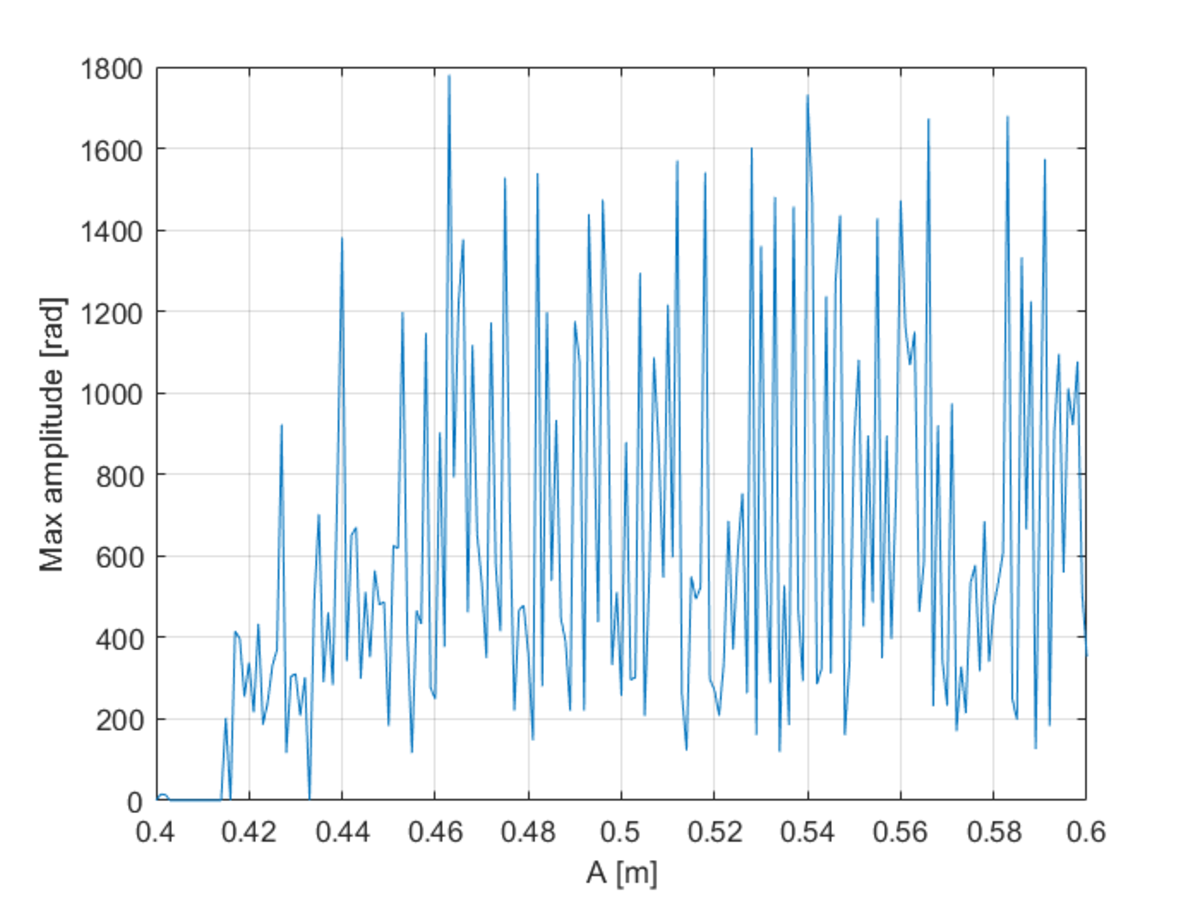
It seems that for large enough amplitudes (>0.3 for our case), the system exhibits some kind of chaotic behavior. Does anyone have an explanation?
The amplitude was varied in steps of 1e-3 m and the numerical integration was performed by the function ode15s in Matlab.
The Lagrangian for this system is given by L = T − V , where T = 2 1 m ( L 2 θ ˙ 2 cos 2 θ + ( A ω cos ω t − L θ ˙ sin θ ) 2 ) and V = m g ( A sin ω t + L cos θ )
Substituting this into the Euler-Lagrange equation of motion, which is,
d t d ( ∂ θ ˙ ∂ L ) = ∂ θ ∂ L
Results in, after simplification,
θ ¨ = sin 2 θ θ ˙ 2 − 4 1 ω 2 sin θ sin ω t + g sin θ
Plugging this into a numerical integrator, (I used Runge-Kutta Fourth-Order method), results in the following deflection angle graph.
The maximum deflection angle comes from the integrator as θ m a x = 1 2 . 7 5 1 ∘ .