Double sum that turns out be harmonic
The equation above holds true for coprime integers and . Find the value of .
Source: Maths Facts
The answer is 28.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Here I wish to share my solution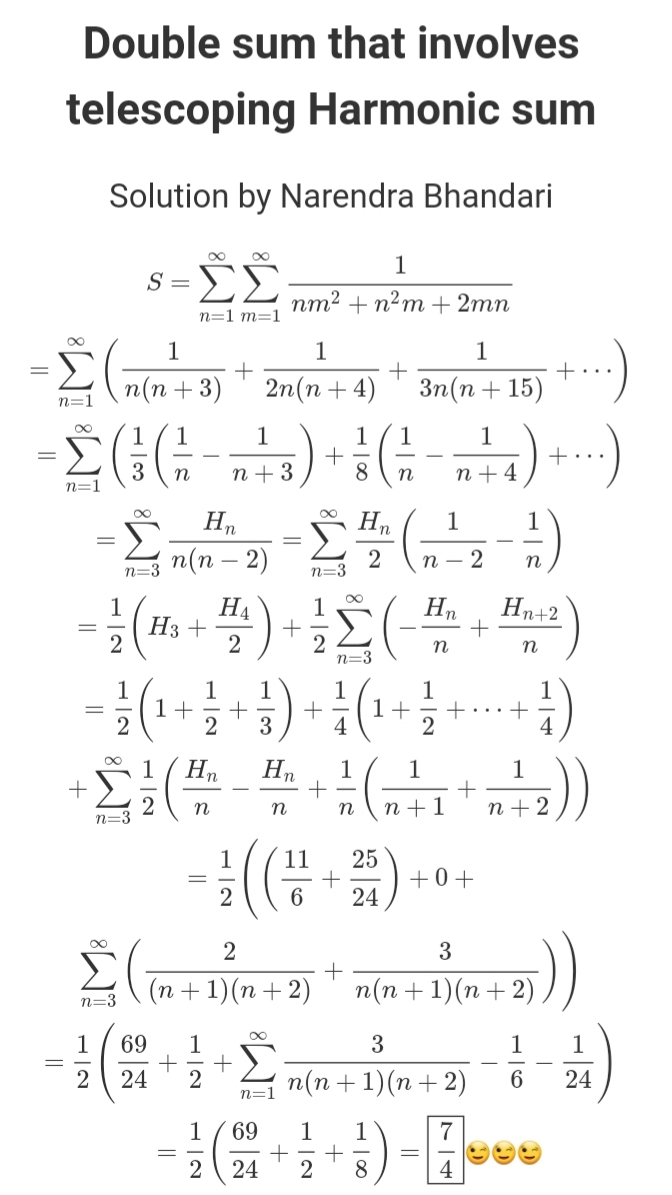
Note that n = 3 ∑ ∞ ( n + 1 ) ( n + 2 ) 2 = 4 2 = 2 1 n = 3 ∑ ∞ n ( n + 1 ) ( n + 2 ) 3 = n = 1 ∑ ∞ n ( n + 1 ) ( n + 2 ) 3 − 6 3 − 2 4 3 = 2 ⋅ 2 ! 3 − 8 5 = 8 1
Note that n m 2 + n 2 m + 2 m n 1 = m n ( m + n + 2 ) 1 = m n 1 ∫ 0 1 x m + n + 1 d x then we have n = 1 ∑ ∞ m = 1 ∑ ∞ m n 1 ∫ 0 1 x m + n + 1 d x = ∫ 0 1 x ( n = 1 ∑ ∞ m = 1 ∑ ∞ m n x m ⋅ x n ) d x = ∫ 0 1 x ln 2 ( 1 − x ) d x = ∫ 0 1 ( 1 − x ) ln 2 x d x hence integrating we have the result 4 7