Double The Paper

Geometry Level 2

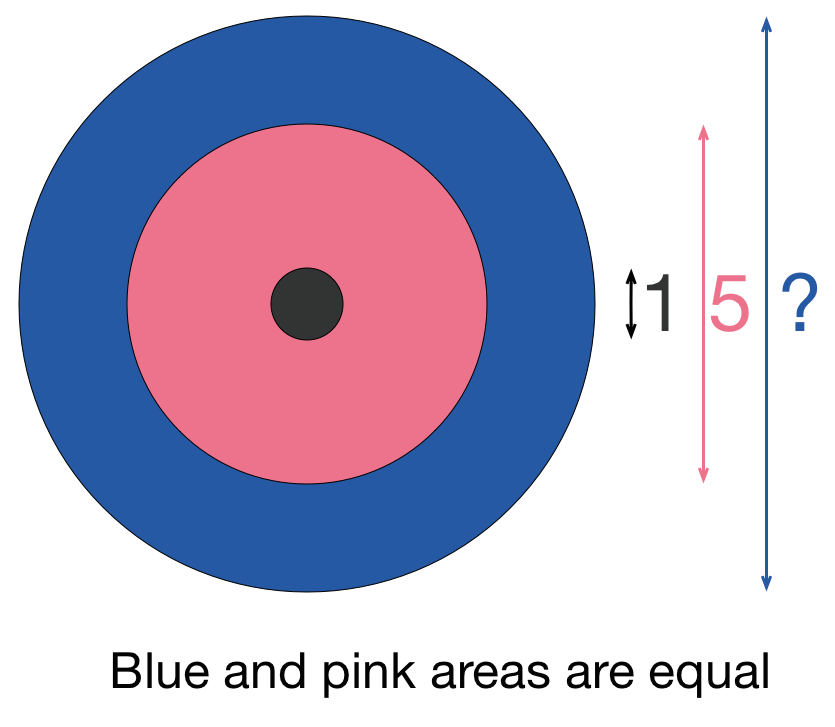
I was shopping for some toilet paper, I saw an advertisment for double the amount of toilet paper as a single roll. Assuming that the toilet paper is equally densely packed, and that the diameter of the core is the same at 1 unit, and the diameter of the original roll is 5 units, what is the diameter of the new roll?

6 7 8 9

2 solutions

Nihar Mahajan
Apr 8, 2016

$\text{Pink Area}=\text{Pink Circle - Black Circle}=\dfrac{25\pi}{4}-\dfrac{\pi}{4}=6\pi$

$\text{Blue Area}=\text{Blue Circle - Pink Circle}=\dfrac{\pi d^2}{4}-\dfrac{25\pi}{4} \\ \text{ where d = diameter of blue circle}$

$\text{Pink Area}=\text{Blue Area} \longrightarrow 6\pi=\dfrac{\pi d^2}{4}-\dfrac{25\pi}{4}$

$\text{Solving for 'd' we have} \ \boxed{d=7}$

Very interesting toilet paper indeed.

Moderator note:

Simple standard approach.

In actuality, they pack it denser, cos otherwise the radius will be too big.

But still, the larger radius makes the toilet paper roll harder to deal with, and it barely fits into my toilet paper holder.

Calvin Lin Staff - 5 years, 2 months ago

Even your toilet paper can be inspiration for someone. XD

Nihar Mahajan - 5 years, 2 months ago

Shoaib Muneer
Apr 27, 2016

let the diameter of new roll = d then

Area of new roll = 2(Area of pink)+Area of black

pi(d/2)^2= 2( pi(5/2)^2 - pi (1/2)^2) + pi(1/2)^2

=> d^2 = 49 => d=7

Double The Paper

2 solutions

Moderator note:

0 pending reports