Double the Trouble
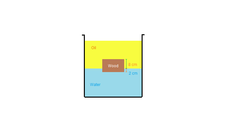 A cubical wooden block floats at the interface between oil and water with
of its length below water and
above it, as shown. If the density of the oil is
, determine the relative density of the block.
A cubical wooden block floats at the interface between oil and water with
of its length below water and
above it, as shown. If the density of the oil is
, determine the relative density of the block.
The answer is 0.68.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Apply the Archimedes' Principle , the weight of the fluids displaced would be proportional to the height immersed in it. So, d × 1 0 = 1 × 2 + 0 . 6 × 8 . Hence the answer d = 0 . 6 8