Double Trouble
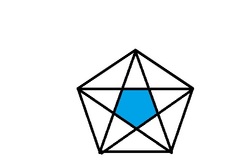 The alternate (interior) angles of a regular pentagon are joined to form another regular pentagon. The ratio of the area of the smaller pentagon to the area of the bigger pentagon in simplest form is
(
a
−
b
×
c
)
:
d
,
where
a
,
b
,
c
,
d
all are pairwise co-prime and
a
>
0
.
Find
a
+
b
+
c
+
d
.
The alternate (interior) angles of a regular pentagon are joined to form another regular pentagon. The ratio of the area of the smaller pentagon to the area of the bigger pentagon in simplest form is
(
a
−
b
×
c
)
:
d
,
where
a
,
b
,
c
,
d
all are pairwise co-prime and
a
>
0
.
Find
a
+
b
+
c
+
d
.
The answer is 17.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
I did the same but using the law of sines:
We have: sin 3 6 ∘ v = sin 7 2 ∘ u ⇒ v = 2 cos 3 6 ∘ u
So that : v = 4 cos 2 3 6 ∘ 1 = 4 1 + tan 2 3 6 ∘
We know that: tan 2 3 6 ∘ = 5 − 2 5
⇒ v = 4 6 − 2 5 = 2 3 − 5
⇒ v 2 = 4 ( 3 − 5 ) 2 = 4 1 4 − 6 5 = 2 7 − 3 5
My way was similar to Mariano's. The triangles that form a pentagram have angles ( 7 2 ∘ , 7 2 ∘ , 3 6 ∘ ) , and the additonal ones that fill in the outer pentagon have angles ( 1 0 8 ∘ , 3 6 ∘ , 3 6 ∘ ) . Some of you may recognise these as the golden triangles, with sides in ratios ϕ : ϕ : 1 and ϕ : 1 : 1 respectively.
As a result, the sides of the inner pentagon are in ratio 1 : ϕ 2 to those of the outer pentagon. Squaring both sides, we get the ratio of their areas, 1 : ϕ 4 . But we need the RHS to be an integer, so let's rewrite it as ϕ − 4 : 1 .
By using the well-known properties ϕ 2 = ϕ + 1 and ϕ − 1 = ϕ − 1 , we can deduce that ϕ − 4 = ( ϕ − 1 ) 4 = ( ϕ 2 − 2 ϕ + 1 ) 2 = ( 2 − ϕ ) 2 = 4 − 4 ϕ + ϕ 2 = 5 − 3 ϕ Substituting ϕ = 2 5 + 1 we deduce that ϕ − 4 = 2 7 − 3 5 so the ratio of areas is 7 − 3 5 : 2 giving 7 + 5 + 3 + 2 = 1 7 .
I did the same! :D
The area of a regular pentagon is A = k ∗ s 2 where s is the side length and k is a constant value. So if we let the side length of the larger pentagon be 1 and the side length of the smaller pentagon be b , then the desired ratio will be b 2 .
Now label 3 vertices of the larger pentagon, starting from the lower right and going clockwise, A , B and C . Also, label 2 vertices of the smaller pentagon, starting from the lowest one then going clockwise, D and E . Let A D = C E = a . Then A B = B C = 1 , and as D E = b we have that A C = 2 a + b .
Now since triangles Δ B E C and Δ C B A are similar, we have that
C E B C = B C A C ⟹ a 1 = 1 2 a + b ⟹ b = a 1 − 2 a 2 .
Now, applying the Cosine Rule to Δ B E C , we have that
1 = a 2 + a 2 − 2 ∗ a ∗ a ∗ cos ( ∠ B E C ) ⟹ 1 = 2 a 2 ( 1 − cos ( 1 0 8 ∘ ) )
⟹ a = 2 ( 1 + cos ( 7 2 ∘ ) ) 1 and 1 − 2 a 2 = 2 a 2 cos ( 7 2 ∘ ) .
This gives us that b = 2 a cos ( 7 2 ∘ ) = 2 ( 1 + cos ( 7 2 ∘ ) ) 2 cos ( 7 2 ∘ )
⟹ b 2 = 1 + cos ( 7 2 ∘ ) 2 cos 2 ( 7 2 ∘ ) .
Now cos ( 7 2 ∘ ) = 4 5 − 1 , so
b 2 = 2 ( 3 + 5 ) ( 5 − 1 ) 2 = 8 2 8 − 1 2 5 = 2 7 − 3 5 .
Thus a + b + c + d = 7 + 5 + 3 + 2 = 1 7 .
I used the fact that sin 1 8 ∘ = 4 1 5 − 4 1 (half of the golden ratio).
Let a be the side of the large pentagon, b the length of the 10 star edges, and c the side of the small polygon.
Then, analyzing the two kinds of isosceles triangle in the situation, a = 2 b sin 1 8 ∘ = ( 2 1 5 − 2 1 ) b ; c = 2 b cos 3 6 ∘ = ( 2 1 5 + 2 1 ) b . (For the latter I used cos 3 6 ∘ = 1 − 2 sin 2 1 8 ∘ . )
Thus the ratio between the pentagon sides is c a = 2 1 5 + 2 1 2 1 5 − 2 1 = ( 2 1 5 − 2 1 ) 2 = 1 2 1 − 2 1 5 ; and the ratio of the areas is the square of this, ( c a ) 2 = ( 1 2 1 − 2 1 5 ) 2 = 2 7 − 3 5 .
Thus the answer is 7 + 3 + 5 + 2 = 1 7 .
The ratios between lineal dimensions of congruent elements of the small pentagon to the big one is the square of the inverse of the Golden Ratio. Therefore the ratio between area will be the fourth power of the inverse of the golden ratio.
(2/(sqrt(5)+1))^4 = (7-3*Sqrt(5))/2.
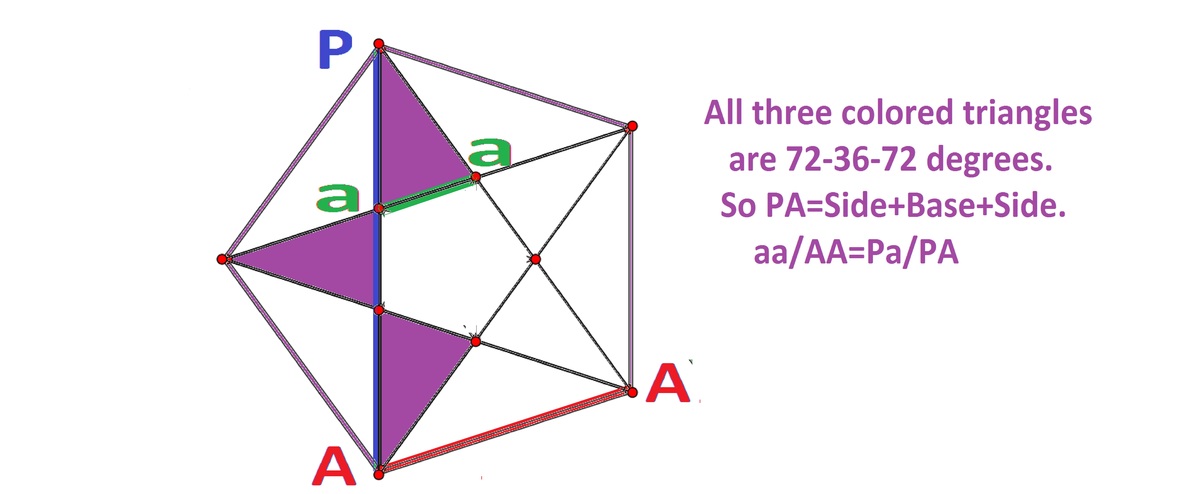
 We take the middle isosceles triangle containing the green small side aa, and Big red side AA.
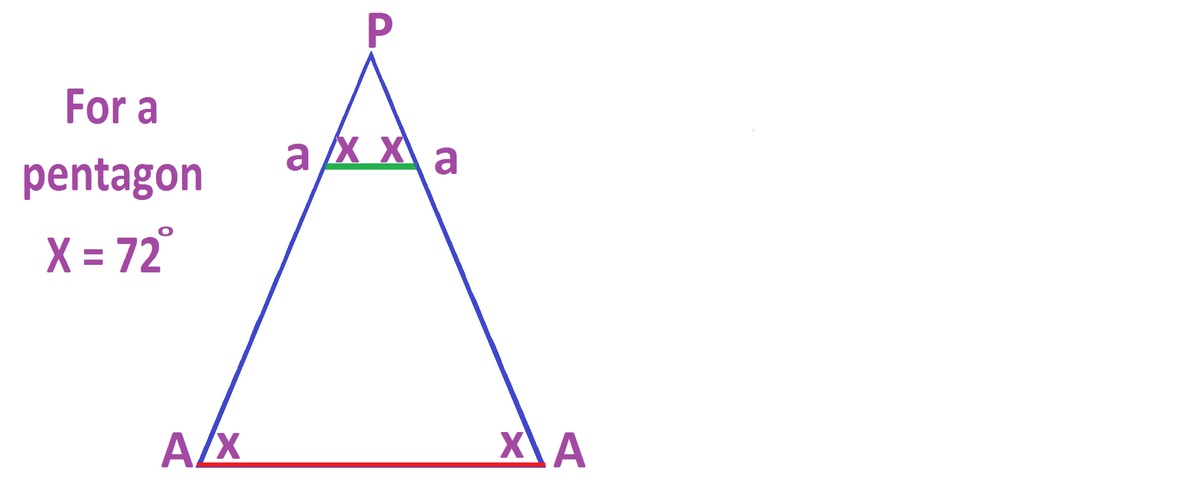
Let Pa=x. For a pentagon,
P
A
=
x
+
2
C
o
s
7
2
∗
x
+
x
=
2
∗
x
∗
{
1
+
4
5
−
1
}
=
x
∗
2
5
+
3
.
B
I
G
A
R
E
A
s
m
a
l
l
a
r
e
a
=
(
B
I
G
S
I
D
E
s
m
a
l
l
s
i
d
e
)
2
=
(
A
A
a
a
)
2
.
=
(
x
∗
2
5
+
3
x
)
2
We take the middle isosceles triangle containing the green small side aa, and Big red side AA.
Let Pa=x. For a pentagon,
P
A
=
x
+
2
C
o
s
7
2
∗
x
+
x
=
2
∗
x
∗
{
1
+
4
5
−
1
}
=
x
∗
2
5
+
3
.
B
I
G
A
R
E
A
s
m
a
l
l
a
r
e
a
=
(
B
I
G
S
I
D
E
s
m
a
l
l
s
i
d
e
)
2
=
(
A
A
a
a
)
2
.
=
(
x
∗
2
5
+
3
x
)
2
WLOG, let the side of the larger pentagon be 2. Each angle of this pentagon is 180(5-3)/5 = 108 degrees. So the upper left triangle has angles 36, 36, and 180 degrees. Thus the right side of this triangle is 1/cos(36). The upper middle triangle has angles 36, 72, and 72 degrees. So its bottom side is r = cos(72)/cos(36) = sin(18)/cos(36) = [sin(18)/[1-2^sin(18)]. And the desired ratio is r^2 : 1. It sufficient to find r.
We have
cos(18) = sin(72) = 2 * sin(36)*cos(36) = 2[2 * sin(18) * cos(18)] * [1-2 * sin^2(18)],
1 = 4 * sin(18) * [1-2 * sin^2(18)],
8 * sin^3(18)-4 * sin(18)+1 = 0,
[2 * sin(18)-1][4 * sin^2(18)+2 * sin(18)-1] = 0,
sin(18) = 1/2 or [-1+/-sqrt(5)]/4.
Since 0 < sin(18) < sin(30) = 1/2, so sin(18) = [-1+sqrt(5)]/4. It follows that
sin^2(18) = [3-sqrt(5)]/8,
r = {[-1+sqrt(5)]/4} / {[1+sqrt(5)]/4} = [3-sqrt(5)]/2,
r^2 = [7-3*sqrt(5)]/2,
r^2:1 = 7-3*sqrt(5) : 2.
Hence a = 7, b = 5, c = 3, d = 2, and a+b+c+d = 17.
Let x be the side length of the smaller pentagon and y be the shortest distance between a vertex of the smaller pentagon and a vertex of the larger pentagon. (So the diagonals have length x + 2 y .) We want to find x 2 .
By similar triangles, we have 1 x + 2 y = x y and x + 2 y 1 = 1 y .
Multiplying these together we get x = y 2 . Plugging into either equation and rearranging gives y 3 + 2 y 2 − 1 = 0
( y + 1 ) ( y 2 + y − 1 ) = 0
y = 2 − 1 + 5
x = 2 3 − 5
x 2 = 2 7 − 3 5
And we're done.
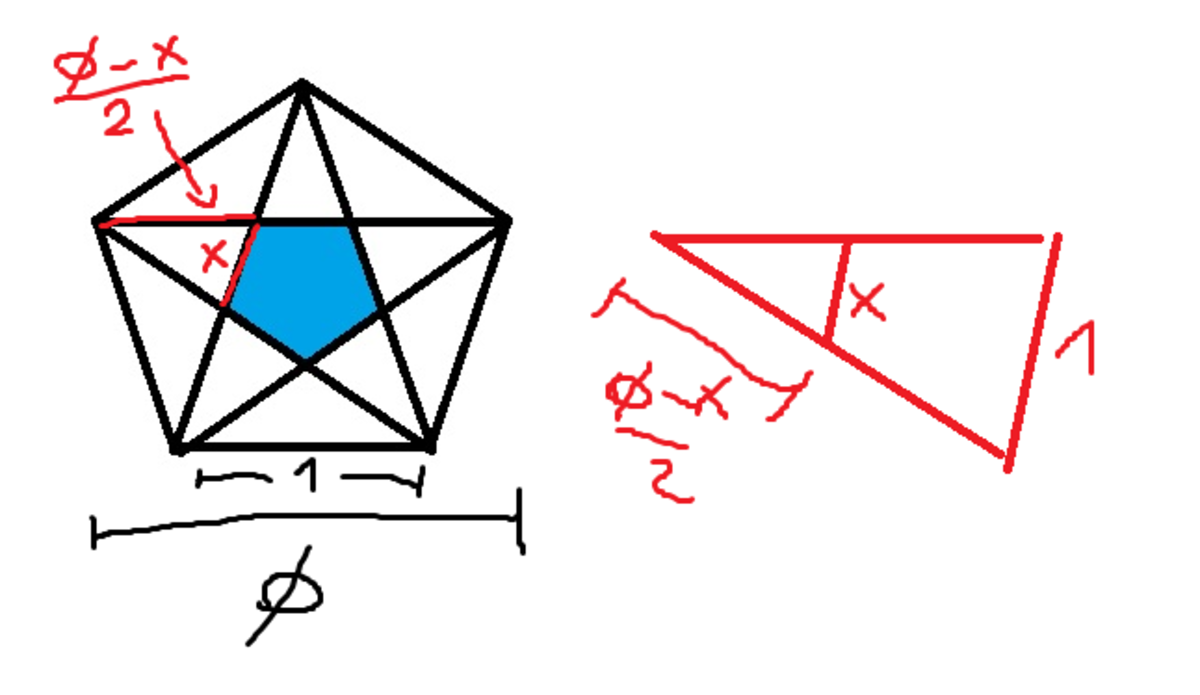
WLOG that the side of a larger regular pentagon is 1 . Using the fact that the ratio of the diagonals and the side of a regular pentagon is ϕ : 1 .
Using similar triangles as shown above, we get: 1 x = ϕ 2 ϕ − x
x = 2 ϕ + 1 ϕ = 2 3 − 5
Therefore, the ratio of the 2 areas is the square of the ratio of their sides = 1 2 x 2 = 2 7 − 3 5 ~~~
Let the side length of the pentagon be 1 , u and v as shown in the figure above. It is noted that all the three angles at a vertex are 3 6 ∘ .
Then, we have: u 2 1 = cos 3 6 ∘ ⇒ u = 2 cos 3 6 ∘ 1
We also have: v = 2 u sin 1 8 ∘ ⇒ v = 2 cos 3 6 ∘ 2 sin 1 8 ∘ = cos 3 6 ∘ sin 1 8 ∘
Now the ratio of areas of the small to big pentagon is: v 2 = ( cos 3 6 ∘ sin 1 8 ∘ ) 2 : 1
And that: cos 2 3 6 ∘ sin 2 1 8 ∘ = cos 3 6 ∘ 2 1 ( 1 − cos 3 6 ∘ )
We know that: cos 3 6 ∘ = 4 1 + 5
⇒ v 2 = ( 4 1 + 5 ) 2 2 1 ( 1 − 4 1 + 5 ) = 1 6 6 + 2 5 8 3 − 5 = 3 + 5 3 − 5 = 4 1 4 − 6 5 = 2 7 − 3 5
⇒ v 2 : 1 ⇒ 7 − 3 5 : 2 ⇒ a + b + c + d = 7 + 5 + 3 + 2 = 1 7