Double Trouble
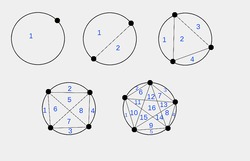 Suppose there is/are
points on the circumference of the circle, define
as the number of pieces for which a circle is divided with these points are joined by chords such that no more than 2 chords intersect at the same point.
Suppose there is/are
points on the circumference of the circle, define
as the number of pieces for which a circle is divided with these points are joined by chords such that no more than 2 chords intersect at the same point.
The diagram above shows that , . Find the value of .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let's find a general formula for f ( n ) by using Eulers theorem.
Eulers theorem is V − E + F = 2 Where V , E and F denote the number of vertices, edges and faces respectively.
f ( n ) = F − 1 since the outside of the circle is also counted as a face.
After finding V and E in terms of n we deduce:
f ( n ) = 1 + 2 4 n ( n − 1 ) ( n 2 − 5 n + 1 8 ) .
f ( 6 ) = 3 1
I would like to note a very similar problem has been posted before and can be found here .
The amazing Otto Bretscher has a solution in which he explains briefly how you can go about finding V and E .
(Where the hell is Otto? He's been inactive for a month and I miss his incredible problems.)