Double Wedge! (Hard Version)
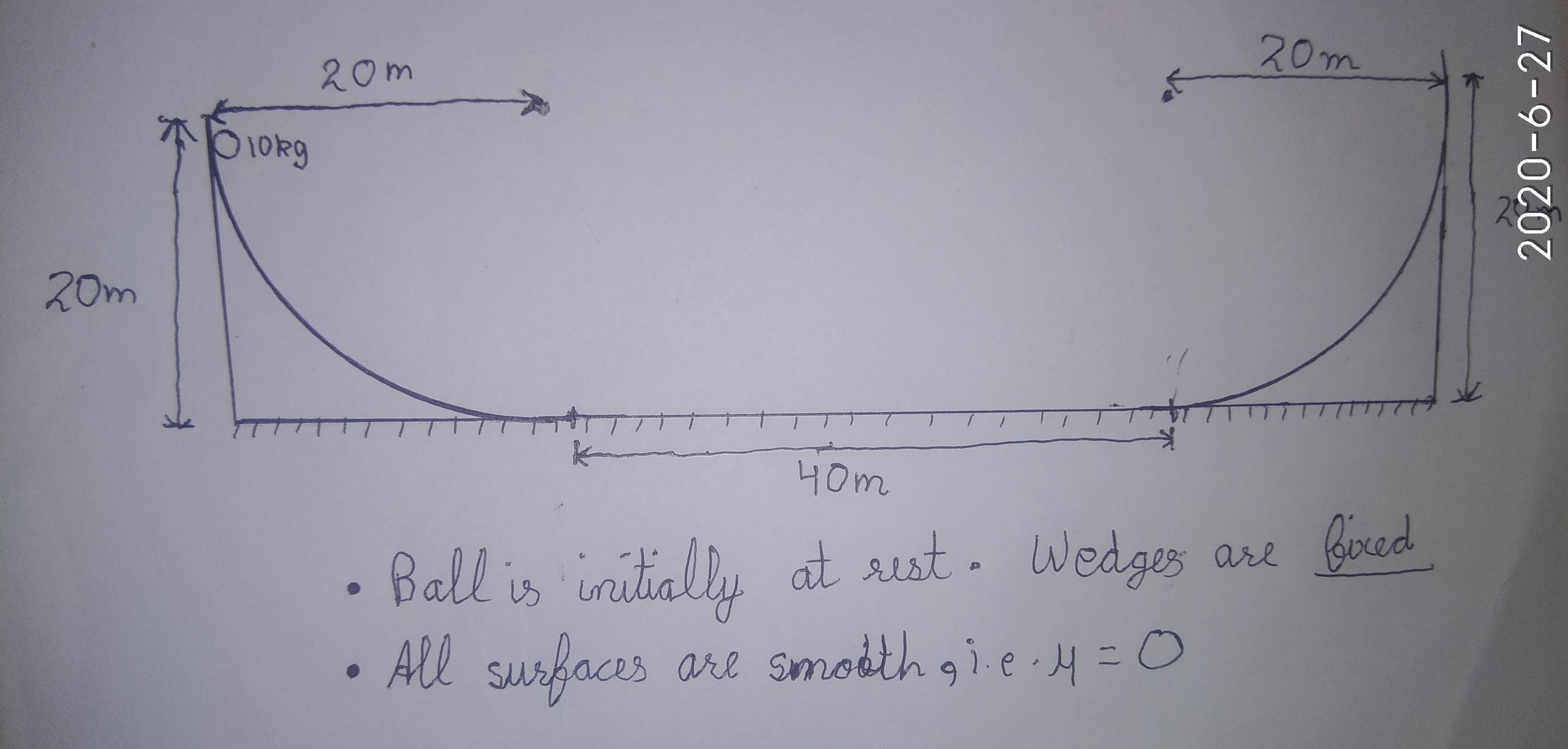
Find the (in second) of the above system(ball), i.e. the time taken by ball to reach the initial point again from start. System is released from rest. For integration value, refer 5th point
Conditions in statement
-
All surfaces are .
-
Wedges are in nature with radius . Distance between wedges is
-
Height of ball from ground is
-
Take acceleration due to gravity
-
Take
My all time inspiration Aniket Sanghi
All of my problems are
Difficulty:
The answer is 14.48.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Time taken to get down the wedge
Using conservation of energy
Now,
Velocity of ball after reaching ground
Time taken to cross road
Time taken to climb second wedge
By symmetry
Time period