Doubling the Angle from the Ladder 2
A ladder on level ground is leaning against a vertical wall. Let L be the length of the ladder, D be the distance from the bottom of the ladder to the wall, H be the distance from the top of the ladder to the ground, and x be the angle formed between the ladder and the ground.
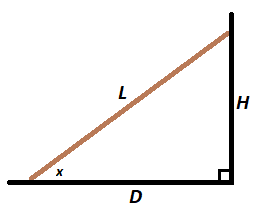
In this problem , we learned that if we double the angle x when L = 2 5 m , D = 2 0 m , and H = 1 5 m , the new distances H ’ and D ’ are also integers.
Not counting sets of measurements that are proportional to the above set of measurements, are there any other sets of measurements which have the property that L , D , H , D ’ , and H ’ are all integers for a doubled angle x ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice solution!
Log in to reply
Thank you! And thanks for sharing this fun problem!
For Pythagorean triplets, let's us take:
D = k ( m 2 − n 2 ) ; H = k ( 2 m n ) , L = k ( m 2 + n 2 ) , where m , n , k ∈ N and m > n
Let t a n ( x ) = D H = m 2 − n 2 2 m n ⇒ x = a r c t a n ( m 2 − n 2 2 m n ) , and 2 x = 2 ⋅ a r c t a n ( m 2 − n 2 2 m n ) . Taking our doubled angle, 2 x , we now obtain:
t a n ( 2 x ) = D ′ H ′ = t a n ( 2 ⋅ a r c t a n ( m 2 − n 2 2 m n ) = 1 − t a n 2 ( a r c t a n ( m 2 − n 2 2 m n ) 2 t a n ( a r c t a n ( m 2 − n 2 2 m n ) = m 2 − n 2 4 m n ⋅ ( m 2 − n 2 ) 2 − ( 2 m n ) 2 ( m 2 − n 2 ) 2 = ( m 2 − n 2 ) 2 − ( 2 m n ) 2 4 m n ( m 2 − n 2 ) . (i)
The expression in (i) requires ( m 2 − n 2 ) 2 − ( 2 m n ) 2 = 0 ⇒ m 2 − n 2 = 2 m n , which is always true for the leg lengths of Pythagorean triplets. Hence, there are infinitely many triplets that satisfy this L , D , H , D ′ , H ′ ∈ N for a doubled angle x .
sin x = L H and cos x = L D
In the new triangle, x would get turned into 2 x , keeping L constant.
Since the expressions for sin 2 x and cos 2 x in terms of sin x and cos x are polynomial functions with rational coefficients, the values of trigonometric functions for double the angle will still be rational.
sin 2 x = 2 sin x cos x = L 2 2 H D = L H ′
cos 2 x = cos 2 x − sin 2 x = L 2 D 2 − H 2 = L D ′
Hence, H ′ = L 2 H D and D ′ = L D 2 − H 2
For every integral Pythagorean triplet, there will be some proportion of it which will have the above two values integral, i.e. for every triplet a , b , c there will be a k a , k b , k c for which the above two values are integral.