Doubling the angle from the ladder
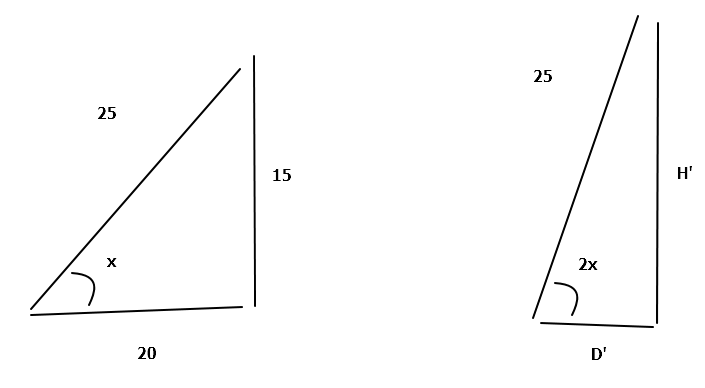
I've placed a 2 5 m ladder on a vertical wall such that its height on the wall H = 1 5 m and its distance from the wall D = 2 0 m .
Now, doubling the angle x between the ladder and the ground, I find that the new height H ′ and new distance D ′ are both integer lengths (in meters) as well!
What is H ′ + D ′ ?
The answer is 31.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Since the information is given that all lengths are integers again, we just have to find another pythagorean triple with a hypothenuse of 25. The only possibility is ( 7 , 2 4 , 2 5 ) , so the answer is 7 + 2 4 = 3 1 .
( 7 , 2 4 , 2 5 ) can be generated by noting that 2 5 = 2 7 2 + 1 . Then, the second leg is 2 7 2 − 1 = 2 4 .
tan ( x ) = 2 0 1 5 = 4 3
Using trigonometric formula tan ( 2 β ) = 1 − tan 2 ( β ) 2 tan ( β )
tan ( 2 x ) = 1 − 1 6 9 2 × 4 3 = 7 2 4
Therefore, H ′ = 2 4 k , D ′ = 7 k
Now, ( 2 4 k ) 2 + ( 7 k ) 2 = ( 2 5 ) 2 ⇒ 6 2 5 k 2 = 6 2 5 ⇒ k = 1
Therefore, H ′ + D ′ = 2 4 ( 1 ) + 7 ( 1 ) = 3 1
25^2 = 625 so need to find 2 integers whose squares sum to 625.
Largest must be less than 25.
24^2 = 576.
625 - 576 = 49.
Sqrt. of 49 is 7.
24 + 7 = 31.
While you have certainly found the correct values, is this the only solution? Why or why not?
For the first angle x , sin x = 2 5 1 5 = 5 3 and cos x = 2 5 2 0 = 5 4 .
For the second angle 2 x , H ′ = 2 5 sin 2 x = 2 5 ⋅ 2 sin x cos x = 2 5 ⋅ 2 ⋅ 5 3 ⋅ 5 4 = 2 4 , and D ′ = 2 5 cos 2 x = 2 5 ( cos 2 x − sin 2 x ) = 2 5 ( ( 5 4 ) 2 − ( 5 3 ) 2 ) = 7 .
Therefore, H ′ + D ′ = 2 4 + 7 = 3 1 .