Doubling the cube
A square of paper is first creased into three equal strips as shown in the diagram. Then the bottom edge is positioned so the corner point P is on the top edge and the crease mark on the edge meets the other crease mark Q .
What is P A P B ?
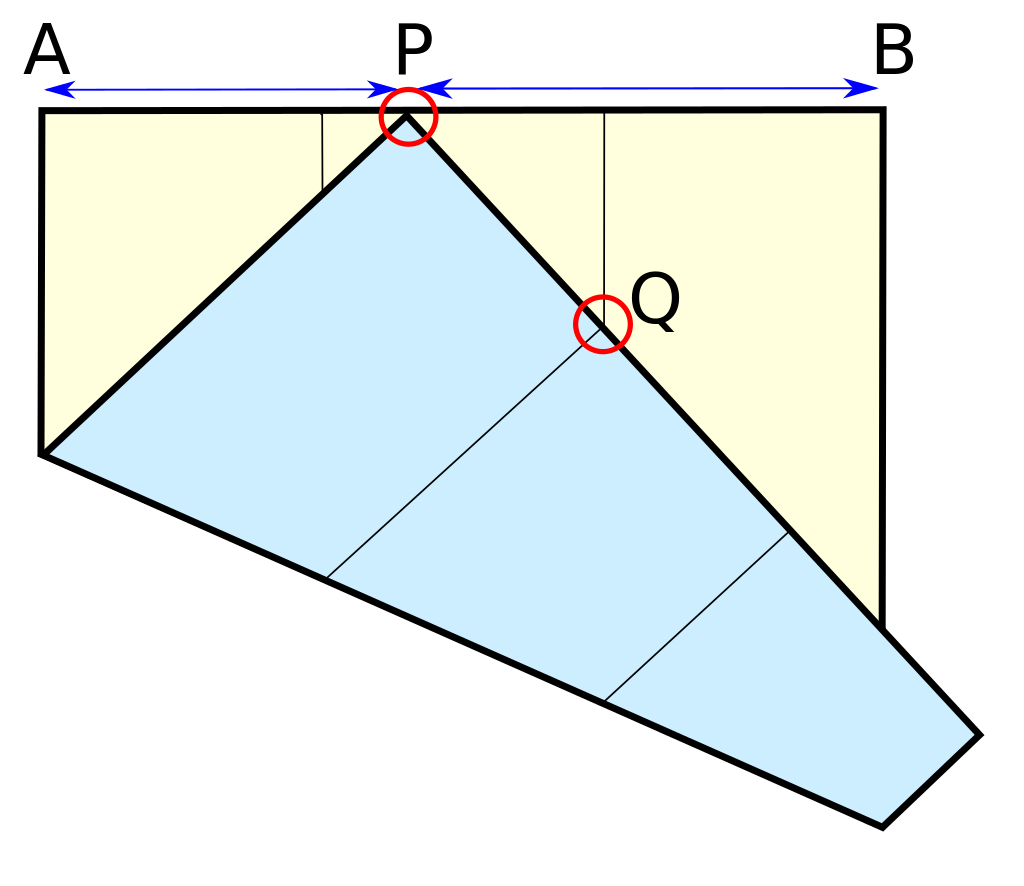
The answer is 1.2599210498948731647672106072782.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
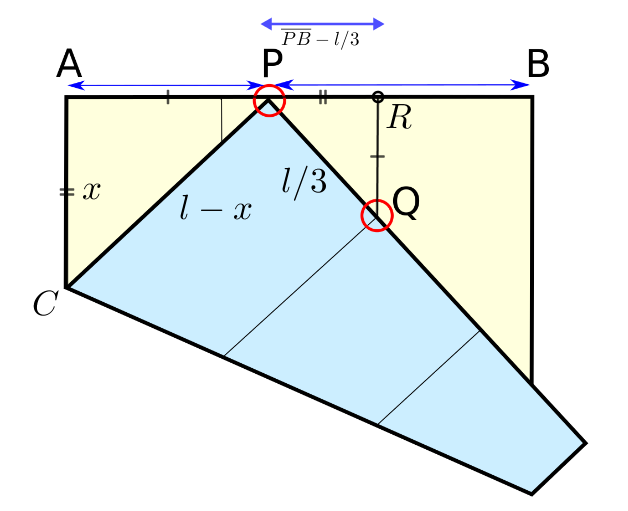
A P 2 = ( l − x ) 2 − x 2 = ( l − x + x ) ( l − x − x ) = l ( l − 2 x ) ⟹ A P = l ( l − 2 x )
B P = l − A P = l − l ( l − 2 x )
Let l = 1 from now on to simplify the expressions. So far we have:
A P = 1 − 2 x ; B P = l − A P = 1 − 1 − 2 x ; A P B P = 1 − 2 x 1 − 1
We now find x noting that triangles △ A C P and △ P R Q are similar:
l − x x = l / 3 B P − l / 3
Being l = 1 and B P = 1 − 1 − 2 x we obtain 1 − x x = 3 ( 1 − 1 − 2 x ) − 1
After some algebraic manipulation, we get the following 3rd-degree polynomial on x and calculate its unique real root*:
1 8 x 3 − 3 6 x 2 + 2 4 x − 5 = 0 ⟹ x = 6 4 − 3 4 ≈ 0 . 4 0 2 1
The desired value is A P B P = 1 − 3 4 − 3 4 1 − 1 ≈ 1 , 2 5 9 9
*It is a laborious task to calculate the root's exact value . I lazily obtained it using Geogebra CAS.
As shown Let P A A C ⟹ P B C P In x 2 + y 2 x 2 y a − y sin θ In P D P E cos ( 9 0 − θ ) sin θ From a 2 + x 2 a 2 − x 2 a 2 + x 2 a 2 − x 2 a ( a 2 − x 2 ) a 3 − a x 2 ⟹ 2 x 3 ⟹ 2 x 3 ⟹ x 3 ( a − x ) 3 ⟹ P A P B by the above figure let the paper be of side length a = x = y = a − x = a − y Δ A C P we have, = ( a − y ) 2 ∠ P A C = 9 0 ∘ = a 2 − 2 a y = 2 a a 2 − x 2 = 2 a a 2 + x 2 = a − y y = a 2 + x 2 a 2 − x 2 ( 1 ) Δ P D E we have, = 3 2 a − x = 3 a = P E P D = 3 a 3 2 a − x ( 2 ) ( 1 ) and ( 2 ) = 3 a 3 2 a − x = a 2 a − 3 x = ( a 2 + x 2 ) ( 2 a − 3 x ) = 2 a 3 − 3 a 2 x + 2 a x 2 − 3 x 3 = ( a 3 − 3 a 2 x + 3 a x 2 − x 3 ) = ( a − x ) 3 = 2 = x ( a − x ) = 3 2 ≈ 1 . 2 5 9 9