Doubly Tangent Line
Let the quartic function be given by
Then, there is a unique line that is simultaneously tangent to the graph of at two distinct points. Let this line be described by
Find .
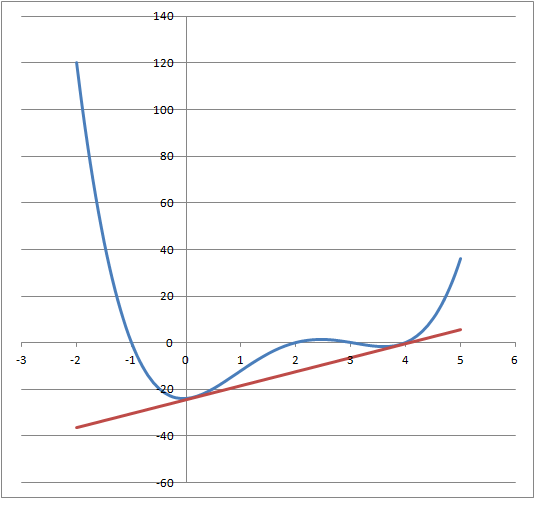
The answer is -18.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let
L ( x ) = m x + b
be the linear function whose graph is tangent to f ( x ) at two distinct points. Define
g ( x ) = f ( x ) − L ( x )
Then, since f ( x ) opens upward, it follows that, f ( x ) has to be above L ( x ) for all x except at the points of tangency, where they are coincident. This means g ( x ) is always non-negative.
Now,
g ( x ) = x 4 − 8 x 3 + 1 7 x 2 + ( 2 − m ) x + ( − 2 4 − b )
Since g ( x ) is non-negative and has two roots, then these two roots must be double roots, and therefore,
g ( x ) = ( x 2 + c x + d ) 2
for specific constants c , d .
Expanding,
g ( x ) = x 4 + 2 c x 3 + ( 2 d + c 2 ) x 2 + 2 c d x + d 2
Comparing the two forms of g ( x ) , we deduce that
c = − 4 , d = 0 . 5 . Hence, m = 6 and b = − 2 4 . 2 5
and, therefore, m + b = − 1 8 . 2 5