Doubly Trisected Triangle
Triangle ABC has ∠ A = 4 0 ∘ , ∠ B = 6 0 ∘ , ∠ C = 8 0 ∘ . Points M , N trisect the side B C and points P , Q trisect the side A C . The lines A M , A N , B P , B Q intersect at the points S , T , U , V as shown in the figure below, dividing the triangle into 9 regions. Determine the smallest possible value of [ A B C ] + [ S T U V ] such that both [ A B C ] and [ S T U V ] are positive integers.
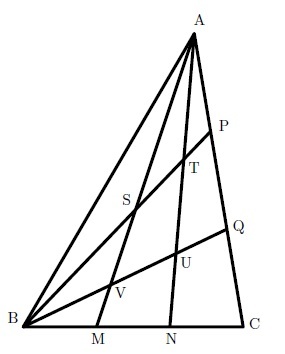
Details and assumptions
[ P Q R S ] refers to the area of figure P Q R S .
The answer is 79.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Draw AR parallel to BC, note the intersection with BS,BV as X,Y. Since AR parallel to BC, so AX:BC=AP:PC=1:2, AY:BC=AQ:QC=2:1. By using intercept theorem several times, we would be able to conclude that BV:VU:UQ=12:9:7, BS:ST:TP=21:9:5. Same thing applies for AS:SV:VM=21:9:5, AT:TU:UN=12:9:7. Hence, the area of STUV over the area of triangle ABC would be (the area of triangle SUV+the area of triangle STU):the area of triangle ABC=[2/3×9/(12+9+7)×9/(9+21)+2/3×9/(12+9+7)×21/(9+21)×9/(9+12)]/1=2×9/140=9/70. Therefore, we can conclude that the smallest possible integral value of [ABC] and [STUV] must be 70 and 9 respectively so the sum of them is 79.
Let h C , h U and h Q be the distance from the vertexes C , U and Q , respectively, to the segment A B ,
Now, we can see that the triangles A B U and N Q U are similar, since Q N is parallel to A B , and the ratio of similarity is 3:1.
From this we have that h U = 4 3 ⋅ h Q = 4 3 ⋅ 3 2 ⋅ h C = 2 1 ⋅ h C .
Using this, we get that [ A B U ] = 2 1 [ A B C ] .
A similar argumente leads to [ A B S ] = 5 1 [ A B C ] , using the similarity of the triangles A B S and M P S and its similarity ratio 3:2.
In particular we have that P S = 5 2 ⋅ B P and A S = 5 3 ⋅ A M .
Now we use the Generalized Angle Bisector Theorem (GABT) in the triangle A C M and we get N M C N = A M A C ⋅ sin ( ∠ N A M ) sin ( ∠ C A N ) .
Since M N = N C , we get A C A M = sin ( ∠ N A M ) sin ( ∠ C A N ) .
We use again GABT in the triangle A P S , we get
T S P T = A S A P ⋅ sin ( ∠ T A S ) sin ( ∠ P A T ) = A S A P ⋅ sin ( ∠ N A M ) sin ( ∠ C A N ) = A S A P ⋅ A C A M = 9 5 .
From this we have that P T = 1 4 5 ⋅ P S = 7 1 ⋅ B P , wich implies that [ A T P ] = 7 1 [ A B P ] and
[ A B T ] = 7 6 ⋅ [ A B P ] = 7 2 ⋅ [ A B C ] .
By symmetry [ A B V ] = 7 2 ⋅ [ A B C ] .
Using all these results we get that [ S T U V ] = [ A B U ] − [ A B T ] − [ A B V ] + [ A B S ] = ( 2 1 − 7 2 − 7 2 + 5 1 ) ⋅ [ A B C ] = 7 0 9 ⋅ [ A B C ] ,
thus, [ S T U V ] is integer if and only if [ A B C ] is a multiple of 70.
So [ A B C ] + [ S T U V ] = 7 0 7 9 [ A B C ] = 7 9 ⋅ k and its smallest value is 79.
Ratio theorem if a cevian divide the side in ratio a/b then the ratio of 2 small triangles are a/b.From menelaus in MAC and transversal PSB we have AS/SM=3/2 ( )and from menelaus in MAC and transversal QVB we have AV/VM=6( ). From( )and( ) we haveAS:SV:VM=21:9:5.In the same way for CAN and the same transversals we get AT:TU:UN=12:9:7.Because its simetric from angle A to B we have BS:ST:TP=21:9:5 and BV:VU:UQ=12:9:7.Now [AVU]=[ABQ] (VU/BQ)=[ABC] (AQ/AC) (VU/BQ)=[ABC] (2/3) (9/28)=[ABC] 3/14.In the same way [AST]=[ABC] 3/35.From this we have [STUV]=[AVU]-[AST]=[ABC] ((3/14)-(3/35))=[ABC]*9/70.And because [STUV]and[ABC] integer and their ratio is 9/70 and we are asked for the smalest integer satisfing the ratio.They are 9 and 70and answer is 70+9=79
The Menelaus Theorem states that when a transversal cuts a triangle at 3 points on the three sides the ratio becomes (-1) so , here in this given problem we take the triangle BCP taking ASM as the transversal , so we get that (BM:MC) (CA:AP) (PS:SB)=(-1) Now putting values of (BM:MC),(CA:AP) as (1:2) and (3:1) respectively we get (PS:SB)=(2:3) again we take the triangle BPC but this time taking ATN as the transversal,so we get that (BN:NC) (CA:AP) (PT:TB)=(-1) Now putting values of (BN:NC),(CA:AP) as (2:1) and (3:1) respectively we get (PT:TB)=(1:6) so aggregating we got (PT:TS:SB)=(5:9:21) Now again this time we take triangle BQC and AVM as transversal , so we get that (BM:MC) (CA:AQ) (QV:VB)=(-1) Now putting values of (BM:MC),(CA:AQ)as (1:2) and (3:2) respectively we get (QV:VB)=(4:3) ,again this time we take triangle BQC and AUN as the transversal ,so we get that (BN:NC) (CA:AQ) (QU:UB)=(-1) Now putting values of (BN:NC),(CA:AQ)as (2:1) and (3:2) respectively we get (QU:UB)=(1:3) so aggregating we got (QU:UV:VB)=(7:9:12) NOW,([PQRS] refers to the area of figure PQRS.)
[STUV]=[AMN] - [AST] - [VUMN], [STUV]=[AMN] - [AST] -{ [AMN] - [AVU] }, [STUV]=(1/3)of[ABC] - (1/3)of[ABC] {(9)/(5 + 9 + 21)} - { (1/3)of[ABC] - (2/3)of[ABC] {(9)/(7 + 9 + 12)} }, [STUV]=(9/70)of[ABC] so,when both [ABC] and [STUV] are positive integers and it is the minimum we get [ABC]+[STUV] = 9+70 = 79
Notice that △ B M U , △ M N U , and △ N C U all have the same area, since they have the same base and height, let this area be x . Similarly, [ A P U ] = [ P Q U ] = [ C Q U ] = y . [ B C Q ] = 3 [ A B C ] = [ A C N ] , so 3 x + y = 3 [ A B C ] = x + 3 y . This gives x = y = 1 2 [ A B C ] , so [ U N C Q ] = 6 [ A B C ] .
If we replace U with S in the above argument, again using areas x , y , we will get that 3 x + 2 y = 3 2 [ A B C ] = 2 x + 3 y . This gives x = y = 1 5 2 [ A B C ] . Since [ A B S ] + [ B M S ] = 3 [ A B C ] , and [ B M S ] = 1 5 2 [ A B C ] , we have [ A B S ] = 5 [ A B C ] .
If we replace S with T and repeat this again, we will find that [ A P T ] = 2 1 [ A B C ] . By symmetry, [ B M V ] = 2 1 [ A B C ] . Since [ A P T ] + [ P T U Q ] + [ C N U Q ] = 3 [ A B C ] , we have [ P T U Q ] = 4 2 5 [ A B C ] . We can similarly deduce that [ B S V ] = 3 5 3 [ A B C ] , and then use these to deduce that [ S T U V ] = 7 0 9 [ A B C ] . For this to be an integer, it must be the case that [ A B C ] is a multiple of 7 0 , which gives [ A B C ] = 7 0 , [ S T U V ] = 9 and [ A B C ] + [ S T U V ] = 7 9 as the smallest possible value.
Note: The equation [ S T U V ] = 7 0 9 [ A B C ] holds for all triangles and is independent of the value of ∠ A , ∠ B and ∠ C .
By using menelaus' theorem on triangle ANC with transversal BP and BQ, we can find that, ST=3/7 BS, TP=5/21 BS, and VU=3/4 BV, UQ=7/12 BV. Let, angle PBQ=ß. Then, [BUT]-[BSV]=[STUV]. By sine rule, we can find that, [STUT]=3/4 BS BV sin ß. Then, Similarly, we can find that, [BPQ]=35/6 BS BV sin ß=1/3*[ABC]. By simple trigonometrical calculation with the informations angle B=60 degree, angle A=40 degree and angle C=80 degree
It is easy to see that if [ A B C ] [ S T U V ] = q p in lowest terms then the minimal value of [ A B C ] + [ S T U V ] , when both terms are positive integers, is p + q . Hence we will find [ A B C ] [ S T U V ] .
Firstly, let CU intersect AB at D. Then by Ceva's Theorem, Q A C Q D B A D N C B N = 1 , so A D = D B and D is the midpoint of AB. Similarly if CS intersects AB at E then E is the midpoint of AB, so D=E, and CUSD is a straight line.
Now by Menelaus's Theorem on triangle CPB and transversal ATN, we have T B P T = A C P A N B C N = 3 1 2 1 = 6 1 , so P B T B = 1 + T B P T 1 = 1 + 6 1 1 = 7 6 .
Thus [ A T B ] = P B T B [ A P B ] = P B T B A C A P [ A B C ] = 7 6 3 1 [ A B C ] = 7 2 [ A B C ] .
Similarly, we can get S C D S = 4 1 , and [ B S C ] = 5 2 [ A B C ] ; also, U A N U = 3 1 , and [ C U A ] = 4 1 [ A B C ] .
Therefore,
[ U T S ] = [ A B C ] − [ A P B ] − [ B S C ] − [ C U A ] = ( 1 − 7 2 − 5 2 − 4 1 ) [ A B C ] = 1 4 0 9 [ A B C ] .
An analogous argument gives [ U V S ] = 1 4 0 9 [ A B C ] , so [ S T U V ] = [ U T S ] + [ U V S ] = 7 0 9 [ A B C ] , and the answer to the original question is 9 + 7 0 = 7 9 .