Doubly Twice!

Geometry Level 3

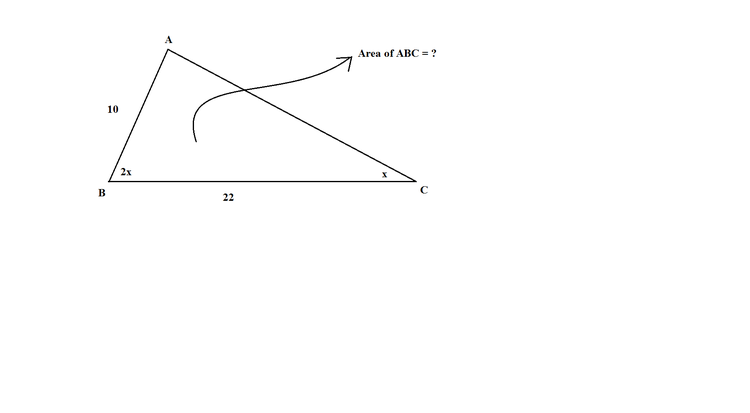In △ A B C \triangle ABC , A B = 10 AB = 10 , B C = 22 BC = 22 . Suppose ∠ B = 2 ∠ C \angle B = 2\angle C . Then find the area of △ A B C \triangle ABC


The answer is 88.

Sagnik Saha by Sagnik Saha , 23, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

4 solutions

Unstable Chickoy
Jun 17, 2014

sin ⁡ ( 180 − 3 x ) 22 = sin ⁡ x 10 \frac{\sin(180 - 3x)}{22} = \frac{\sin{x}}{10}

x = 26.565 x = 26.565

A = 0.5 ( 10 × 22 ) sin ⁡ ( 2 × 26.565 ) = 88 A = 0.5(10\times 22)\sin (2\times26.565) = \boxed{88}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Use the mirror to solve this

0 Helpful 0 Interesting 0 Brilliant 0 Confused

My washroom mirror ?? Pls explain :) :)

Chirayu Bhardwaj - 5 years, 6 months ago
Triptesh Biswas
Apr 15, 2014

Applying b^2=c(c+a) we get area=88

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Sagnik Dutta
Feb 21, 2014

Appling Law of sines to the triangle ABC.......we get... sin x=1/(5^(1/2))..... therefore Area of the triangle ABC= 1/2 * 10 * 22 * sin2x.....= 88 ..(Ans.)

0 Helpful 0 Interesting 0 Brilliant 0 Confused

For an added challenge, try to find a non trigonometric solution! ;)

Sagnik Saha - 7 years, 3 months ago

Well i may give a hint which might be very useful. Think of Δ = 1 2 × base × height \Delta = \frac{1}{2} \times \text{base} \times \text{height}

Sagnik Saha - 7 years, 3 months ago

is this correct........? .. Construction : A line segment is drawn from C to the extended side BA....cutting it at P.......such that angle PCA and angle ACB .are equal.....= x... therefore triangle PCB is an isosceles triangle.... Let PA be termed as a.....therefore PB=PC =(10+a)...... Appling Angle BIsector theorem ...we get... a=(25/3)......Now let perpendiculars AL and PM be drawn on the base BC from vertex A and P respectively.... .. It can be perceived that triangle BAL and triangle BPM are similar............thereby application of the converse of similarty theorem yields BL = 6... therefore AP= 8 ...... [ABC]= 1/2 * 22 * 8= 88 square units...(Ans)

Sagnik Dutta - 7 years, 3 months ago

chesta krchi....! :P

Sagnik Dutta - 7 years, 3 months ago

Can anyone help with the non trigonometric solution??

Aditya Patil - 7 years, 3 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...