Orange Juice Puzzle
 I have a pint of orange juice. I drink half of it and then give it to you. You drink half of what's remaining, and then pass it back to me. I drink half of what's remaining and then give it to you.
I have a pint of orange juice. I drink half of it and then give it to you. You drink half of what's remaining, and then pass it back to me. I drink half of what's remaining and then give it to you.
If this process continues forever, how much of the pint will I drink?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
OMG!! Everyone goes by second method... But the first one is simply amazing!! And u r still 15.. Hats off bro!!! :D
Log in to reply
yep the first method is amazing
S= 1/4 + 1/16 + 1/64 .......... = (1/2^2) + (1/2^4) + (1/2^6) +....... <=> 16S = 4 + 1 + (1/2^4) + ....... <=> 16S = 5 + S <=> 15S = 5 <=> S = 1/3
So I have a problem somewhere..
S= 1/4 + 1/16 + 1/64 .......... = (1/2^2) + (1/2^4) + (1/2^6) +....... <=> 16S = 4 + 1 + (1/2^4) + ....... <=> 16S = 5 + S <=> 15S = 5 <=> S = 1/3
So I have a problem somewhere..
Log in to reply
Your series is not the series of the problem. The series of the problem is 2 1 + 8 1 + 3 2 1 + … , because at the begining you drink 2 1 , and you don't drink 4 1 .
Yes, it is simple: Let's say you drink x 1 , x 2 , x 3 , x 4 , … , so your friend drinks 2 x 1 , 2 x 2 , 2 x 3 , 2 x 4 , … . In total you drink x 1 + x 2 + x 3 + x 4 + … , which is 2 ( 2 x 1 + 2 x 2 + 2 x 3 + 2 x 4 + … ) , that is, in total you drink two times what your friend drinks in total.
Technically, you would never actually drink quite 2/3, and your friend would never quite drink 1/3. -Just sayin
This process of drinking juice is goes to infinite time ,as I drink half then u drink half of half I drink, when only atom of juice left ,I drink half of atom juice and then u drink half of half atom and it still goes on
Let a be the amount that "I" drink. Therefore a = 2 1 + 8 1 + 3 2 1 + 1 2 8 1 + . . .
If we multiply a by 4 , we get 4 a = 2 + 2 1 + 8 1 + 3 2 1 + 1 2 8 1 + . . .
Subtracting the two equations, 3 a = 2 ⇒ a = 3 2
the best soluiton
Log in to reply
why does it have to multiply by four?
Log in to reply
Because the denominators are in multiples of four. You could have multiplied if by any other multiple of four and it would still work.
Oh my friend, do you know that what you are doing is actually using sum of geometric sequences. You method comes from the calculation of recurring decimal or derivation of sum of geometric sequences
Why has to be 4? And... 2 f.e.?
The second person always drinks half of what first one drank. so 2:1 => 2/(2+1) = 2/3
This is simple question. First of all, you should modelling this problem into mathematics form. You have to focus on that question, the subject is "I". So, We count the total of pint that "I" drank.
First time, "I" drink a half of orange juice, so it was 2 1 , then "I" give back the juice to you. I drink it again, but it's a half of you drink, so it was 4 1 ∗ 2 1 = 8 1 . This event happen again and next "I" drink 3 2 1 , approximate to infinite. The solution is Infinite Geometric Series , you can check at this .
Finally, the a is 2 1 and the rasio, r is 4 1 . Total of pints that "I" drink is S ∞ = 1 − r a = 1 − 4 1 2 1 = 3 2 . The answer is 3 2 . :)
Agree thumbs up
A more detailed solution (almost the same with Trevor B's solution, but with more details).
The problem says that I drink half of the juice, give it to you, then you drink half of what's remaining. Then you pass it back to me and I drink half of what you've left, and then I give it back to you again. Then the process goes on forever.
Let S 1 be the amount of juice I drank in pints, and S 2 be the amount of juice you drank in pints. Given these, it then follows that: S 1 = 2 1 + 8 1 + 3 2 1 + . . . S 2 = 4 1 + 1 6 1 + 6 4 1 + . . .
We can see from the equations above that S 2 is just half of S 1 , so factoring 2 1 out from S 2 , we will get: S 2 = 2 1 ( 2 1 + 8 1 + 3 2 1 + . . . )
It now somehow looks like the first equation S 1 , therefore: S 2 = 2 1 S 1
We can now combine these into a single equation: S 1 + 2 1 S 1 = 1 2 3 S 1 = 1 3 S 1 = 2 S 1 = 3 2
And there you have it, I have drunk 3 2 pint of juice.
I did the same thing.
your explanation is the best
There are two ways to approach this problem. If you note that Person 1 (the "I" in the problem) drinks 1/2 pint, then 1/8 pint, then 1/32 pint, etc., then you can apply the formula for the sum of an infinite geometric series S that has first term a and common ratio r. In this problem a = 1/2 and r = 1/4, since Person 1 drinks 1/2 pint the first time and 1/4 of the previous amount each successive time: S = 1 − r a = 1 − ( 3 / 4 ) 1 / 2 = 3 2
You can also approach this problem by noting that Person 1 always drinks twice as much as Person 2 (the "you" in the problem). For example, Person 1 drinks 1/2 pint, then Person 2 drinks 1/4 pint. When Person 1 drinks 1/8 pint, then Person 2 drinks 1/16 pint. As the process continues forever, the total amount of orange juice drank by the two people will approach 1 pint. If Person 1 always drinks twice as much as Person 2, then Person 1 should drink 2/3 pints.
r= 1/4 not 3/4
The amount the person drinks can be represented as follows.
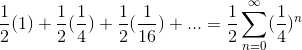 Since (1/4)<1, the amount he drinks is:
Since (1/4)<1, the amount he drinks is:
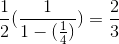
Moderator note:
Good solution.
And Kudos for pointing out that ∣ r ∣ < 1 hence the geometric progression sum could be applied.
This is a problem for which we should first know about the infinite GP series. For an infinite GP, sum ( S ) = 1 − r a where a = First term and r = Common ratio and r < 1 .
I drink at first 2 1 of a pint, then you drink 4 1 of a pint, then again I drink 8 1 of a pint and this goes on. This is an infinite GP with a = 2 1 and r = 4 1 for my drinking parts.
Total pints I drank = 2 1 + 8 1 + 1 6 1 + . . . . ∞
= 1 − 4 1 2 1 = 4 3 2 1 = 2 1 × 3 4 = 3 2
Let you drink x much of the pint, we have:
x 2 x 2 x 2 x 4 x 3 x x = = = = = = = 2 1 + ( 2 1 ) 3 + ( 2 1 ) 5 + ⋯ 1 + ( 2 1 ) 2 + ( 2 1 ) 4 + ( 2 1 ) 6 + ⋯ 1 + ( 2 1 ) 2 ( 1 + ( 2 1 ) 2 + ( 2 1 ) 4 + ( 2 1 ) 6 + ⋯ ) 1 + 4 1 ( 2 x ) 2 + x 2 3 2
∴ You drink two-thirds of the pint.
Trevor B's solution is terrific. I took advantage of the multiple choice aspect of the problem. I start with 1/2 and go up from there so it's not D. You start with 1/4 and go up from there so it's not C. After the second sip, I've had 5/8 and go up from there so it's not B. Thus A.
I drink at first 1/2 of juice next turn i drink,1/8 So it is in a GP 1/2+1/8+1/32+............. Sum =1/2(1/(1-1/4))) =2/3 L a T e X
First, he drinks 1/2 of the juice then 1/8th, then, drinks 1/32. This forms a GP continuing till infinity where a=1/2, r=1/4 Therfore , S(n)=a/(1-r)= (1/2)/(1-1/4)= 2/3
It's simple. The answer can be obtained by analysing the given choices.
∑ i = 2 ( i n f i n i t y ) (1/2)^(n-1) - (1/4)^(n-1)
You drink 2 1 of it. Your friend drinks 4 1 of it. You drink 8 1 of it, and this pattern will continue.
Whenever you drink X amount of it, your friend will then drink 2 X of it. You drink twice the amount your friend does, so the answer is the solution to the equation x + 2 x = 1 , which has the solution x = 3 2
Alternate solution: The amount you drink is an infinite geometric sequence with first term 2 1 and ratio 4 1 . The total amount you drink is equal to the sum of this geometric sequence. 1 − 4 1 2 1 = 4 3 2 1 = 3 2