Dr. Fiendish 3
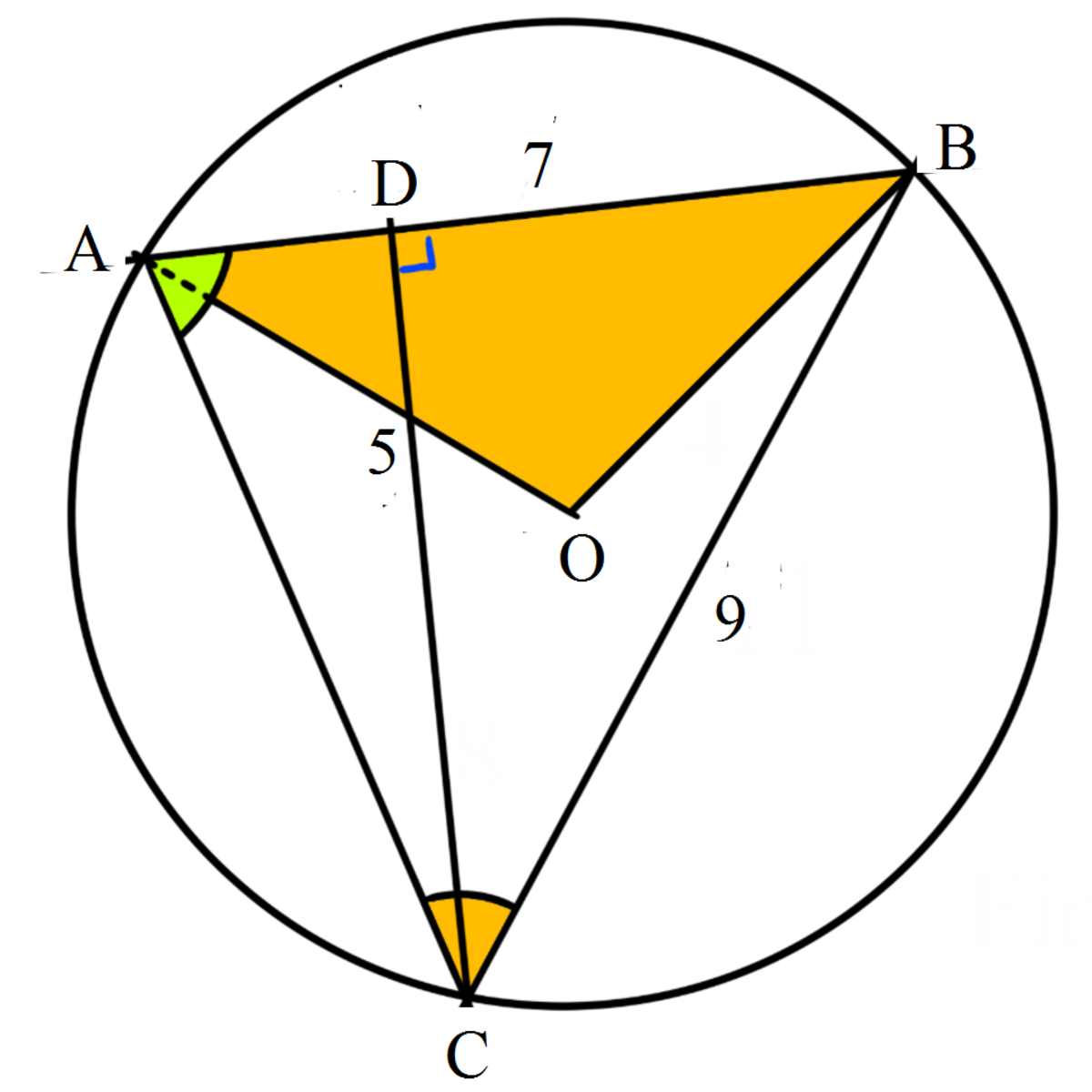
This figure shows the flowerbed in Dr. Fiendish’s garden. Given that O is the center of the circle, B A ⊥ C D , O is in △ A B C , the lengths of A B , O A , and B C are respectively 7 , 5 , and 9 , find ∠ C A B in degrees and the length of C D . Input your answer as the sum of both values.
The answer is 72.688730598383.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Further explanation: Let M be the midpoint of COB. Then cos(angle OCM) = 4.5/5, so angle OCM = 25.842... and angle COM = 90 - angle OCM = 90 - 25.842... = 64.158... Angle COB is 2 * angle COM, but since the angle at the centre is twice the angle on the circumference, angle CAB = (1/2) * angle COB = angle COM = 64.158... Your method doesn't use the cosine and sine rule which is impressive.
Since ∠ A C B is at the circumference and ∠ A O B at the center extended from the same chord A B , ∠ A C B = 2 1 ∠ A O B and sin ∠ A C B = 5 3 . 5 = 0 . 7 . By sine rule , we have:
9 ∠ C A B sin ∠ C A B ⟹ ∠ C A B = 7 ∠ A C B = 9 ⋅ 7 0 . 7 = 0 . 9 ≈ 1 . 1 1 9 7 6 9 5 1 5 rad ≈ 6 4 . 1 5 8 ∘
Then we have
C D = B C sin ∠ A B C = 9 sin ( π − ∠ A C B − ∠ C A B ) = 9 sin ( ∠ A C B + ∠ C A B ) = 9 sin ( sin − 1 0 . 7 + sin − 1 0 . 9 ) = 9 ( 0 . 7 1 − 0 . 8 1 + 0 . 9 1 − 0 . 4 9 ) = 9 ( 0 . 7 0 . 1 9 + 0 . 9 0 . 5 1 ) ≈ 8 . 5 3 1
Therefore the answer is 6 4 . 1 5 8 + 8 . 5 3 1 ≈ 7 2 . 7 .
@Jeff Giff , don't use such a huge font size for letters and numbers. You are crowding up the figure. Don't need to enter so many space at the end to go to next line. Just key in Enter. Don't use P.S. for note. It is only used in letter writing. Don't worry about decimal place. Although you specified very high accuracy but the system takes only three significant figure as shown in under answer boxed. For this problem, I think from 72.6 to 72.8 is consider correct. I have edited your problem wording. Thanks.
Log in to reply
Thank you! By the way, I have tried only typing enter but it doesn’t work. Is it because I am using mobile version? Thanks! :)
BTW, you forgot to close the brackets in the 11 & 12th lines :)
Hello @Chew-Seong Cheong , are you a moderator at brilliant. How can I become one? Thanks in advance!!
I don't know, it was decided by Brilliant.
@Jeff Giff , please don't change back the image. Letters A , B , C , D , and O should be small. The image was redone by me.
Note that we have to check that whether
O
is in
△
A
B
C
, as the question requires so.
Apply
the cosine rule
on
△
A
B
O
.
7
2
=
5
2
+
5
2
(
r
a
d
i
i
,
O
A
=
O
B
)
−
2
×
5
×
5
cos
∠
B
O
A
.
⇒
cos
∠
B
O
A
=
0
.
0
2
,
∠
B
O
A
=
cos
−
1
0
.
0
2
=
8
8
.
8
5
4
0
0
8
…
∘
and since
angle at center is twice angle on circumference
,
∠
B
C
A
=
2
∠
B
O
A
=
4
4
.
4
2
7
0
0
4
…
∘
Now apply
the sine rule
on
△
A
B
C
.
A
B
=
7
sin
∠
B
C
A
=
0
.
7
=
B
C
=
9
sin
∠
C
A
B
⇒
∠
C
A
B
=
sin
−
1
0
.
9
=
6
4
.
1
5
8
0
6
7
2
3
6
8
3
3
…
∘
Now let’s find
C
D
. Note that
C
D
is the height on
A
B
. Hence we have to find the area of
△
A
B
C
, by using
the sine rule
or
the cosine rule
and applying
S
t
r
i
a
n
g
l
e
=
a
b
sin
C
=
4
R
a
b
c
=
2
r
(
a
+
b
+
c
)
or
Heron’s formula
. I would suggest using
S
=
a
b
sin
C
because it only requires the angle ABC.
So the area of
△
A
B
C
=
5
9
.
7
1
4
6
4
3
5
3
0
8
5
…
⇒
C
D
=
7
5
9
.
7
1
4
6
4
3
5
3
0
8
5
…
=
8
.
5
3
0
6
6
3
3
6
1
5
5
…
Check!
O
is in
△
A
B
C
.
So the answer is
6
4
.
1
5
8
0
6
7
2
3
6
8
3
3
…
+
8
.
5
3
0
6
6
3
3
6
1
5
5
…
=
7
2
.
6
8
8
7
3
0
5
9
8
3
8
3
…
.
@Brilliant Mathematics please change the answer into 72.688730598383, because I inserted the wrong number in the calculator 😅
Log in to reply
Thanks. I've updated the answer.
Or simply change it to 72.68873😊 thx
What I did was applied the extended law of sines to get the angles of the triangle and use that to find the length of CD
Overview of a (Bashy) Solution: We are given two sides of the triangle, and can figure out the third side from the formula 4 R a b c = a r e a . From there, use Pythagorean Theorem to find C D , and trigonometry to find ∠ C A B .
Step 1: Find A C .
Let A C = x . Then we have
4 R a b x = a r e a
Using Heron's formula for the right side gives
4 ⋅ 5 x ⋅ 7 ⋅ 9 = 2 2 1 ⋅ ( 1 6 + x ) ( x − 2 ) ( x + 2 ) ( 1 6 − x )
Solve to get x ≈ 9 . 4 7 8 5 . . . or x ≈ 3 . 3 7 6 0 5 . . .
Step 2:Pythagorean Theorem on Δ A D C and Δ C D B to find C D
Let A D = w .
Then we have the two equations
x 2 − w 2 = C D 2
9 2 − ( 7 − w ) 2 = C D 2
Solving we have w = 1 4 x 2 − 3 2 , so the only choice of x that makes w positive is x ≈ 9 . 4 7 8 5 .
Plugging in,
w ≈ 4 . 1 3 1 5 8 so
C D = x 2 − w 2 ≈ 8 . 5 3 0 6 6
Step 3: Find ∠ C A B .
tan ∠ C A B = w C D = 4 . 1 3 1 5 8 8 . 5 3 0 6 6
∠ C A B = 6 4 . 1 5 8 0 6 ∘
Summing, 8 . 5 3 0 6 6 + 6 4 . 1 5 8 0 6 ≈ 7 2 . 6 8 8 7
That was amazing! How did you create a graph true to scale? What app did you use? Thank you! :)
App is called "Math Illustrations." It's a program that is suitable for coordinate geometry problems mostly. But, it will compute algebraic expressions too.
Log in to reply
Oh. Thanks for letting me know! :)
cos ∠ O B C = 0 . 9 ⟹ ∠ O B C ≈ 2 5 . 8 4 2 ° ⟹ ∠ B O C ≈ 1 2 8 . 3 1 6 ° ⟹ ∠ C A B ≈ 6 4 . 1 5 8 °
cos ∠ O B A = 0 . 7 ⟹ ∠ O B A ≈ 4 5 . 5 7 6 ° ⟹ ∠ A O B ≈ 8 8 . 8 4 9 ° ⟹ ∠ A C B ≈ 4 4 . 4 2 4 ° ⟹ ∠ A B C ≈ 7 1 . 4 1 8 °
∣ C D ∣ = 9 sin ∠ A B C ≈ 8 . 5 3 1
Hence the required answer is 6 4 . 1 5 8 + 8 . 5 3 1 = 7 2 . 6 8 9 .