Drag & Friction - Part 2

Referring to the first part's solution ( https://brilliant.org/problems/drag-friction/?ref_id=1608702 ):

$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad v(t) = \frac{mg (\sin \theta - \mu \cos \theta)}{b}(1-e ^{-\frac{b}{m}t}) + v_{0}e ^{-\frac{b}{m}t}$

Substituting numerical values :

$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad v(t) = 4-3e^{-\frac{1}{2}t}$

$$

$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad v_{ss} = 4 \ m/s \ \ce{->} \ \frac{5}{8}v_{ss} = 2.5 \ m/s$

Substitute the speed to $v(t)$

$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad 4-3e^{-\frac{1}{2}t} = 2.5$

$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad t = 2 \ln 2$

Integrate $v(t)$ to get the distance $s$ covered by the object :

$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad s = \int_{0}^{2 \ln 2} (4-3e^{-\frac{1}{2}t}) \ dt = 4(2 \ln 2) + 6e^{-\ln 2} - 0 - 6 = 8 \ln 2 - 3$

Look at the figure below :

Positions of the object

Notice that :

$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad s \sin \theta = (1-\alpha) H$

$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \alpha = 1 - \frac{s \sin \theta}{H} = 1 - \frac{0.5(8\ln 2 -3)}{100} \approx 1 - 0.012725 = 0.987275 \approx 0.987$

Therefore,

$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \boxed{\alpha = 0.987}$

Summary of Steps:

• Derive Equation of Motion

• Solve for the velocity $v$ of the object w.r.t time

• Find the time $T$ taken to reach the desired speed

• Solve for the position $x$ of the object w.r.t to time

• evaluate $x(T)$

• Determine $\alpha$

See free body diagram for an illustration of the forces acting on the body.

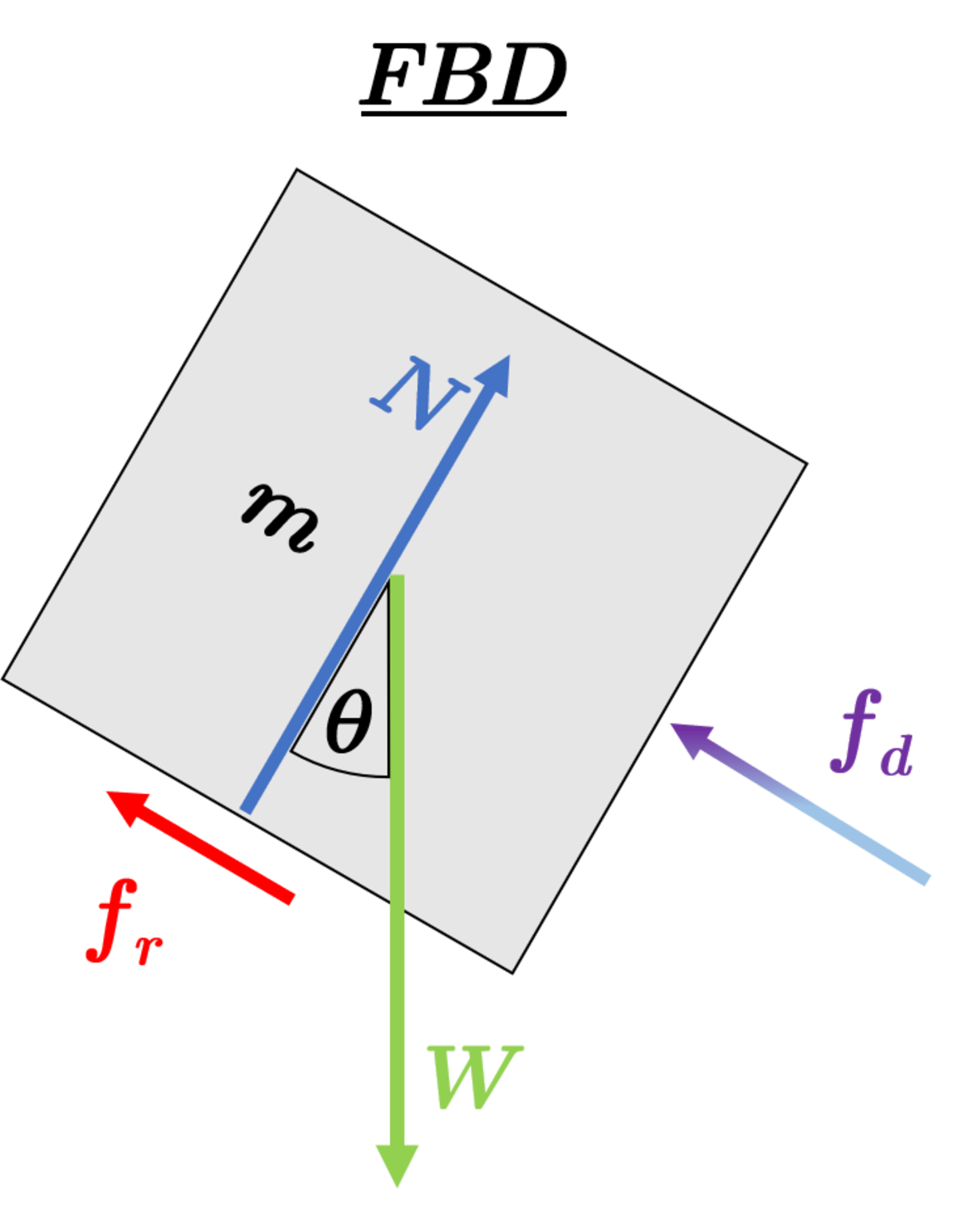
We can use Newtons Second Law to Derrive the equations of motion

$\displaystyle \sum F_x=\ m\frac{dv}{dt}=mg\sin{\theta}\ -\ \mu mg\cos{\theta}-\ bv$

Dividing through by the mass of the body $m$ :

$\displaystyle \frac{dv}{dt}=g\left(\sin{\theta}\ -\ \mu\cos{\theta}\right)-\ \frac{b}{m}v$

Introduce new constants $\beta$ and $\tau$ to clean up the differential equation:

$\displaystyle\beta=\ g\left(\sin{\theta}\ -\ \mu\cos{\theta}\right)$

$\displaystyle\tau=\ \frac{m}{b}$

The resulting First Order Non-Homogeneous Linear ODE is as follows:

$\displaystyle \frac{dv}{dt}=\ \beta\ -\ \frac{1}{\tau}v\$

One method to solve the above equation is shown below:

Let

$\displaystyle \varphi=\ \beta\ -\ \frac{1}{\tau}v$

Then differentiating $\varphi$ w.r.t $v$

$\displaystyle \frac{d\varphi}{dv}=\ -\ \frac{1}{\tau}$

Using the Chain Rule:

$\displaystyle \frac{d\varphi}{dt}=\frac{d\varphi}{dv}\frac{dv}{dt} = -\ \frac{1}{\tau}\varphi\$

We now have reduced the differential equation to type to Seprable.

The solution in terms of $\varphi$ is as follows:

$\displaystyle \frac{\varphi_f}{\varphi_o}=\ e^\frac{-t}{\tau}$

Switching variables back to velocity $v$ :

$\Large v(t) = \left( v_o - \tau \beta \right) e^{ \frac{-t}{ \tau}} + \tau \beta$

Now we can determine the steady state solution ( terminal velocity ):

$\displaystyle v_{ss}=\lim_{t\rightarrow\infty}{v(t)}\ =\tau\beta$

Now we can solve for the time $T$ to reach the target velocity in terms of $v_{ss}$

$\displaystyle \frac{5}{8}v_{ss}\ =\frac{5}{8}\ \tau\ \beta\ = \left( v_o - \tau \beta \right) e^{ \frac{-t}{ \tau}} + \tau \beta$

$\displaystyle T\ =\ -\tau\ \ln{\left(\frac{3}{8}\frac{\ \tau\beta}{\left(\tau\beta\ -\ v_o\right)}\right)}$

Now, find the position $x(t)$ by intgrating $v(t)$ w.r.t. $t$ :

$\Large \begin{aligned} x(t) &= \int{v(t) dt} \\ &=\int \left( \left( v_o - \tau \beta \right) e^{ \frac{-t}{ \tau}} + \tau \beta \right) dt \\ & =\ \tau\left(\beta\ t\ -\ \left(\tau\ \beta\ -\ v_o\right)\left(1\ -\ e^\frac{-t}{\tau}\ \right)\right) \end{aligned}$

Now we can substitute the time $T$ taken to reach $\frac{5}{8} v_{ss}$ :

$\displaystyle x(T)\ =\ \tau\left(v_o+\ \tau\beta\left(\ln{\left(\frac{8}{3}\frac{\left(\tau\beta\ -\ v_o\right)}{\tau\beta}\right)\ -\ \frac{5}{8}}\right)\right)\approx\ 2.545\ \text{m}$

Finally , we can deterermin $\alpha$ ( the fraction of the initial height $H$ ) to be:

$\Large \alpha=\ 1\ -\ \frac{x(T)}{H}\sin{\theta}\approx\ 0.987$