Dragged
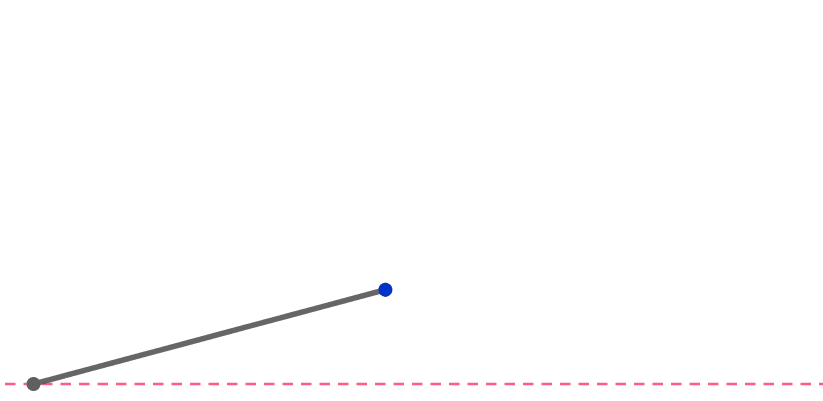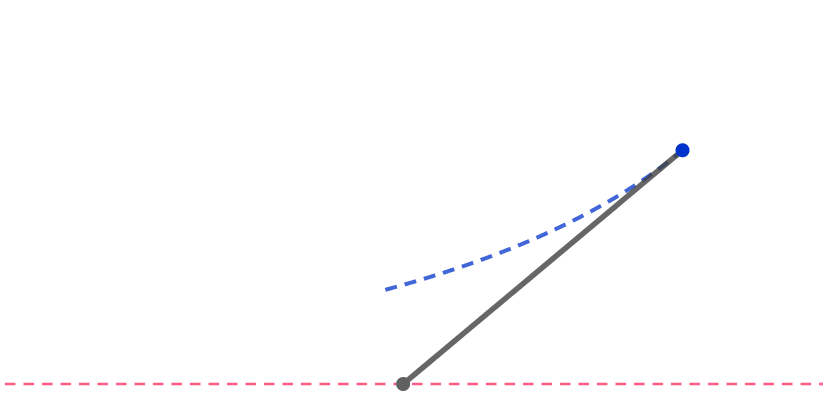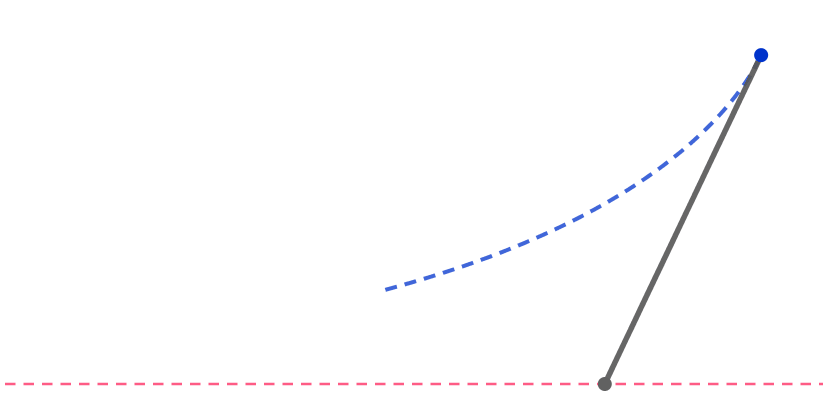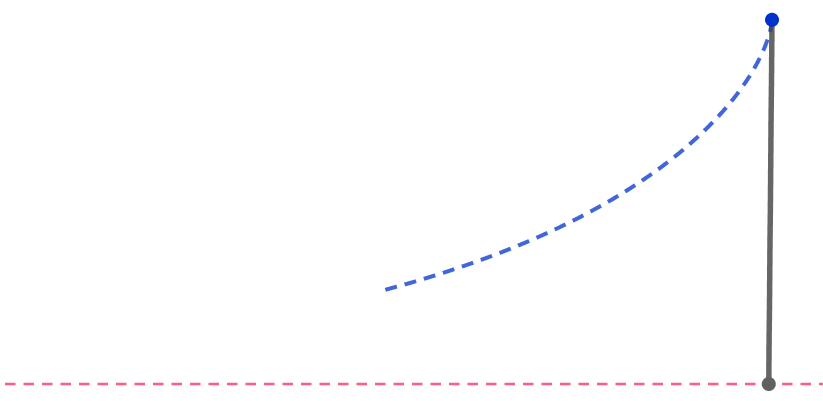
A pen of unit length is lying tilted on a rough table.
The lower end of the pen is dragged in the horizontal direction until the pen becomes vertical. During this process, the upper end of the pen travels a unit distance.
How many units does the lower end travel?
Assume that the velocity of the upper end of the pen is always parallel to the pen.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Certainly the solution that I could understand better than the previous one.
Suppose that the lower end of the rod has travelled a distance X at the moment that the rod makes and angle of θ with the horizontal, and that the initial value of θ is α . The coordinates of the upper end of the rod are ( X + cos θ , sin θ ) and we shall assume that the roughness of the table means that the upper end of the rod always moves in a direction that is parallel to the rod. Thus we must have ( X ′ − sin θ cos θ ) = d θ d s ( cos θ sin θ ) where s is the distance travelled by the upper end of the rod. Thus d θ d s = cos θ X ′ − sin θ = sin θ cos θ and hence d θ d X = c o s e c θ d θ d s = cot θ Thus the distances travelled by the two ends of the rod, during the motion α ≤ θ ≤ 2 1 π are X = [ − ln ( c o s e c θ + cot θ ) ] α 2 1 π = ln ( c o s e c α + cot α ) 1 = s = [ ln ( sin θ ) ] α 2 1 π = ln ( c o s e c α ) Thus c o s e c α = e , so that cot α = e 2 − 1 , and so X = ln ( e + e 2 − 1 ) .
This is the tractrix. Parameterized by the position of the lower end of the rod with 0 at the cusp: x ( t ) = t − tanh ( t ) ; y ( t ) = \sech ( t ) ; Arc length is s ( t ) = lo g ( cosh ( t ) ) . Solving s ( t ) = 1 we get t = lo g ( e + e 2 − 1 )
Roughness of the table has nothing to do with it. If the upper point simply rotates around the lower point, then the lower point does not have to move at all. That works on both rough and smooth surfaces. This problem cannot be solved without taking the parallel movement assumption directly from the diagram.
Log in to reply
Yes I thought the same, it would have to be explained in the inital statment
I posted a very similar problem, see https://brilliant.org/problems/dragging-a-rod/?ref_id=1507333. The main difference is that we do not need to require that the upper end will move parallel to the rod. That follows from the condition that the net torque around the lower end is zero.
could you help me understand how the first equation comes about? why is ds the distance travelled by the upper end of the rod? Thank you!
Log in to reply
Parameterized by the angle theta, you can always express the velocity as a magnitude times direction; here the magnitude is ds/dtheta and the direction is the same as the rod (cos theta, sin theta)
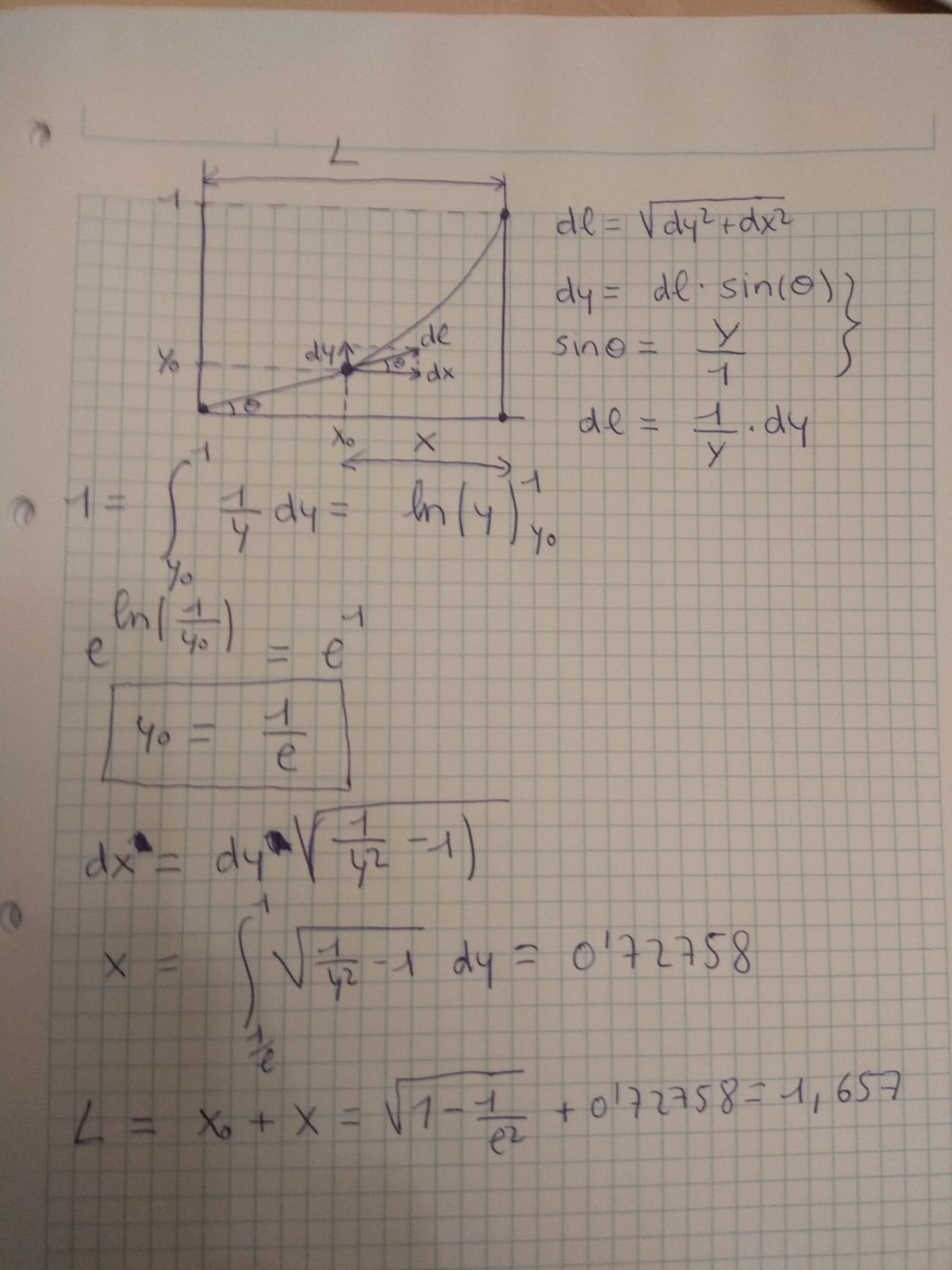 It is a little messy but I just wanted to make sure I didn't commit any mistakes.
It is a little messy but I just wanted to make sure I didn't commit any mistakes.
The answer is in the question: Thanks to the dotted lines the creator provided, the answer should be approximately equal to 41/25, which is 1.64. The correct answer is 1.657454454... I know this solution is not appealing, but it gets the job done! :)
I recognized this curve as a tractrix, which I came across in an undergrad course on ODEs. Funny what sticks even after 40+ years. So I looked up the solution on Wolfram (I did solve it way back then), but it took me a while to realize that we wanted the dog walker's distance, not the horizontal distance traveled by the dog. If the dog reference is confusing, apparently it is common in German to call it a "hundekurve" link text . In my ODE book the dog was replaced by a small boat on smooth water. That was a nice way to physically satisfy the tangency condition.
We will call the distance the bottom of the pen moves x , the distance the top of the pen moves p , the angle of the pen θ , and the initial angle of the pen α .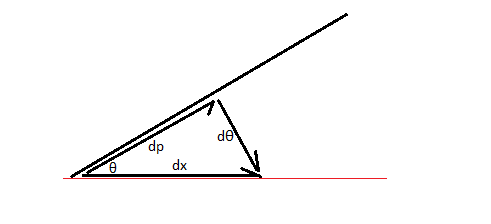
When we move the bottom of the pen d x , it will move the tip d p (parallel to the pen) and rotate the bottom of the pen d θ as shown. We are interested in finding x, so we can use θ as our parameter to get x = ∫ θ = α 2 π d x Using the diagram, this is equal to ∫ θ = α 2 π csc ( θ ) d θ All we have to do now is find α . Because the tip of the pen moves a unit distance, 1 = p = ∫ θ = α 2 π d p = ∫ θ = α 2 π cot ( θ ) d θ Solving the second integral for α ( α = arcsin ( 1 / e ) ), and plugging that into the first integral gives us x = ln ( e + e 2 − 1 )