Dragging a Rod

The pulled end of the rod will move with constant velocity, and its coordinates will be $x_1=v_0t$ and $y_1=0$ , where $\ell$ is the length of the rod. For the rest of the discussion we will assume the $v_0 \rightarrow 0$ limit i.e. the motion is "slow and steady".

The free end has coordinates of $x_2=\ell \cos \alpha+x_1$ and $y_2=\ell \sin \alpha$ , where $\alpha$ is the angle between the rod and the black line. Taking the time derivative and using $\omega =\dot \alpha$ , $v_x=\dot x_2$ , $v_y=\dot y_2$ we get

$v_x=-\omega \ell \sin \alpha +v_0$ , $v_y=\omega \ell \cos \alpha$

The velocity of the free end makes an angle $\beta$ to the reference line so that $\sin \beta= v_y/v$ and $\cos \beta= v_x/v$ , where $v=\sqrt{v_x^2+v_y^2}$ The magnitude of the friction force is constant, $F$ . The direction of the friction force is opposite to the velocity:

$F_x=-F\cos\beta$ , $F_y=-F\sin\beta$

For the equation of motion we need to look at the torque acting on the rod and make it equal to zero. Using the pulled end as the axis of rotation, we get

$F_x\ell \sin \alpha= F_y \ell \cos \alpha$

Inserting the friction force and the velocity expressed before, we get

$\left(-\frac{\omega \ell}{v_0}\sin \alpha +1\right)\sin \alpha= \frac{\omega \ell}{v_0} \cos^2\alpha$

or

$\sin \alpha=\frac{\omega \ell}{v_0}=\frac{\dot \alpha \ell}{v_0}$

This is a first order differential equation, that can be solved by separation of variables:

$\frac{v_0}{\ell}dt=\frac{d\alpha}{\sin \alpha}$

The integration yields

$\frac{v_0}{\ell}t= \log (\tan \alpha/2) +const$

The time is related to the position of the pulled end by $t=x/v_0$ , therefore

$\frac{x}{\ell}= \log (\tan \alpha/2) +const$

It turns out that if const =0 then at $x=0$ we have $\alpha=90^{\circ}$ . When $x=\ell$ , we get $\tan \alpha/2 = e$ , and we can solve that for $\alpha$ . Recalling that $y_2=\ell \sin \alpha$ we get $y_2=0.648$

Ivo Zerkov (see below) pointed out that the response can be written in the form of $\frac{2e}{1+e^2}$ .

The red curve below shows the position of the top of the rod as the bottom is pulled. A few instances of the positions of the full rod are also shown.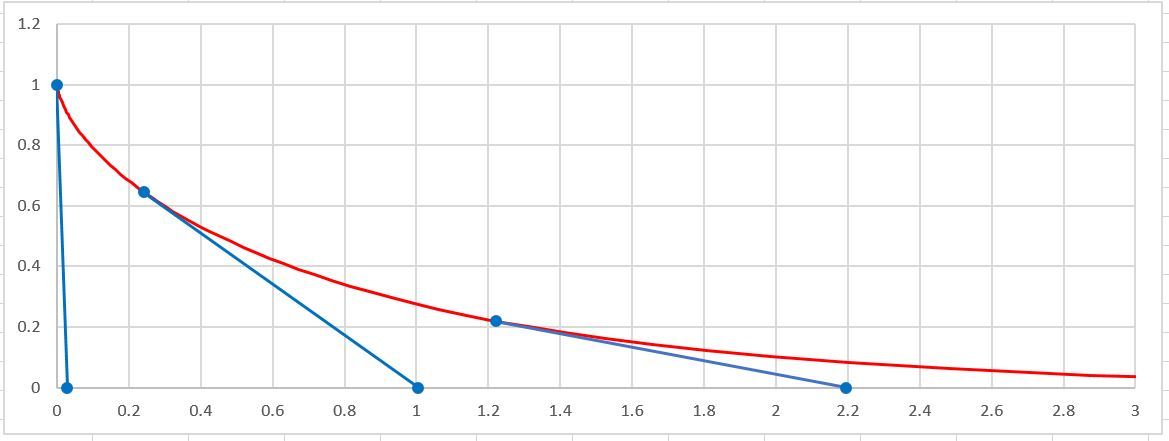

Notes:

1. The motion is reversible. If we start with a rod that is nearly parallel to the reference line, and pull it backwards, the free end will follow the same curve.

2. One of the consequences of the torque equation is that $\alpha=\beta$ . The motion of the end point of the rod is parallel to the rod, just as in this problem

3. It is not necessary to require that the friction is the same everywhere. As long as the friction is isotropic (independent of the direction of motion) the result is the same.

Here's a numerical simulation. Interestingly, I consistently get about 0.648, instead of 0.645. I'm using very high resolution for the simulation. But close enough, I suppose.

import math
import random

#####################################

m = 1.0  # mass and length
L = 1.0

I = (1.0/3.0) * m * (L**2.0)  # moment of inertia

g = 10.0 # gravity

mu = 0.1 + 0.5 * random.random() # randomly generated friction coeff

W = m*g  # weight

t = 0.0  # time and time resolution
dt = 10.0**(-4.0)

v = 0.001  # very low velocity for dragging point
tf = 1.0 / v  # final simulation time

#####################################

theta = math.pi / 2.0   # theta initially 90 deg
thetad = 0.0   # first and second derivatives
thetadd = 0.0

#####################################


while t <= tf:

    theta = theta + thetad * dt      # numerical integration
    thetad = thetad + thetadd * dt

    x = v*t + L * math.cos(theta)    # free end coordinates and velocity
    y = L * math.sin(theta)

    xd = v - L * math.sin(theta) * thetad
    yd = L * math.cos(theta) * thetad

    ########

    vend = math.hypot(xd,yd)  # free end speed

    ux = xd / vend   # unit vectors corresponding to free end velocity
    uy = yd / vend

    ########

    Fx = -mu * (W/2.0) * ux    # friction forces on end
    Fy = -mu * (W/2.0) * uy

    ########

    rx = x - v*t   # lever components for torque calc
    ry = y - 0.0

    ########

    T = rx*Fy - ry*Fx   # torque

    thetadd = T / I   # second deriv of theta

    ########

    t = t + dt  # increment time

#####################################

# print results

print t
print theta
print x
print y