Draw it in one go
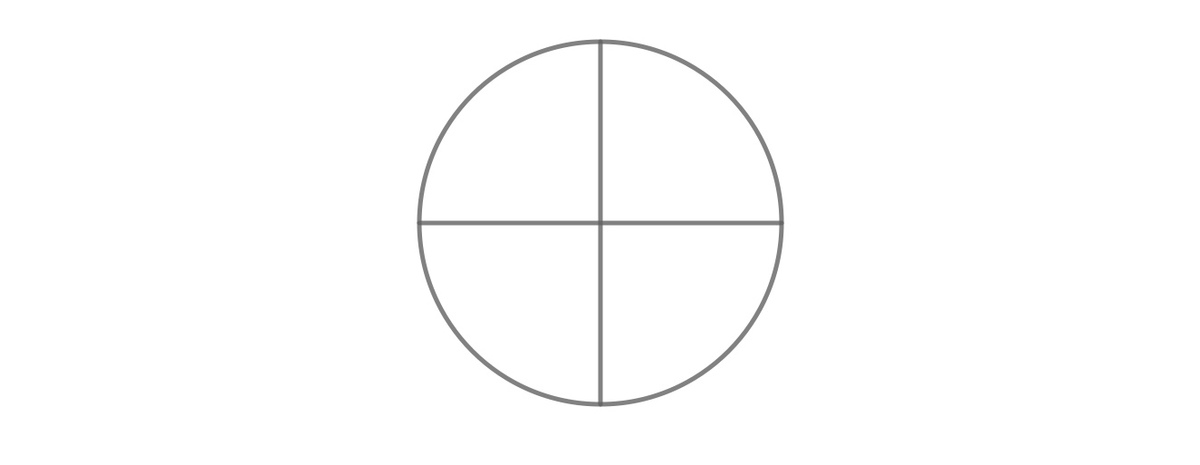 Can we draw the pattern above in one go? "One go" means each segment is traced at once, and your pen cannot leave the paper.
Can we draw the pattern above in one go? "One go" means each segment is traced at once, and your pen cannot leave the paper.
To be precise, using following rules to draw it:
1. You can start at anywhere on the figure.
2. You cannot lift your writing tool once you have started tracing.
3. You cannot trace over any segment more than once.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I dont want to sound pedantic, but I think this would only count as a complete soluition if you said if and only if or just only if . By what you wrote, you are saying that # of vertices with odd # of edges ≤ 2 ⇒ has eulerian path But that doesn't imply right away that # of vertices with odd # of edges > 2 ⇒ doesn’t have eulerian path
The way I answered this problem without knowing about Eulerian Path is using symmetry to reduce the number of possibilities.
Here how it goes, First, I started from any point on the circumference of the circle and I tried my best to draw the picture in one go (I failed of course), then I noticed that I will fail regardless of the direction I go (providing that I started from a point on the circumference) because the circle is symmetric.
This left me with one starting point which is the center, I started at the center going to the left and again trying my best to draw the picture in one go and as expected I failed, then I noticed that when you reach the circumference, the situation is symmetric so it does not matter if you change your initial choice of direction as long as you failed once!
The net result is that you cannot draw this picture in one go.
I am not sure if this is a rigorous argument but it worked!
Log in to reply
I think it would be rigorous, as long as you cover every possibility (and the use of symmetry reduces it dramatically indeed)
But it is no where said that you cannot retrace any curve
Good point, Arnav. In fact this could be used as a trick question after everybody saying no you can reveal that there was no such restriction as you assumed.
Like I mentioned no tricks more or less how it was intended or specified.this situation what we call brain teasers in hopes to think outside the box.what I'm doing playing .to en
In graph theory, an Eulerian trail (or Eulerian path) is a trail in a finite graph that visits every edge exactly once (allowing for revisiting vertices). - Wikipedia
This image does not have an Eulerian path because the lines would overlap if you were to attempt to draw it with 'one go'.
We want to draw the picture in one go. So, take any vertex as starting point then we have to go through every edge and vertices and then we come back to the starting vertex. In this process when we enter any intermediate vertex (that is except the starting vertex) then there must be another edge to leave the vertex. So every intermediate vertex must be of even degree(degree of a vertex means number of edges incident with that vertex) . Also the starting and ending vertex is same hence it is also of even degree. Hence all the vertices must be of even degree. But the picture has vertices of odd degree.
Very an amazing
I'm was surprised about it
It's make my knowledge more large
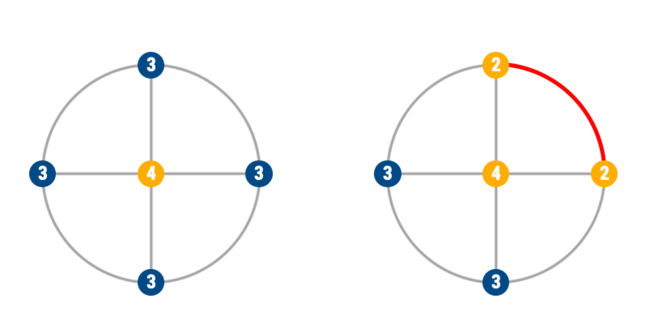
The diagram on the left shows us the degree of each vertex. To trace a path, it should have a maximum of 2 odd degree vertices. In the diagram on the left, we have 4 odd degree vertices, hence it is impossible. To make it possible, a connecting edge (colored in red) between two odd degree vertices should be removed. This makes both of their degrees even.
The best we can do is trace all but one segment, hence the answer is no
A graph has an Eulerian path if it has no more then two vertices with odd number of edges. Here we have four of them, so the answer is no.