Drawing and Measuring is Prohibited
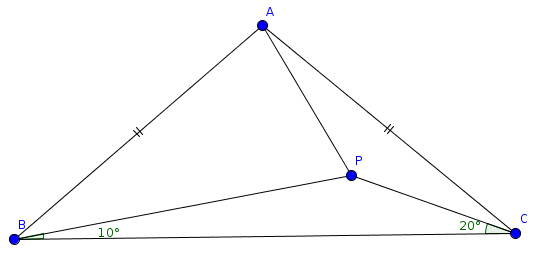
△ A B C is an isosceles triangle with m ∠ B A C = 1 0 0 ∘ and A B = A C . B P and C P intersects at P , with ∠ C B P = 1 0 ∘ and ∠ B C P = 2 0 ∘ . Find ∠ C A P , in degrees.
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Since angle ABC= angle ACB, both must be=(180 - 100)/2=40. so angle ABP=30, and angle ACP=20. L e t A B = A C = x , A P = y , ∠ A P B = M , ∠ A P C = N . ∴ M + N = 1 8 0 − 1 0 − 2 0 = 1 5 0 . ⟹ M = 1 5 0 − N . Applying Sin Law in the form S i n Q S i n P = q p , t o Δ s A B P a n d A C P . S i n M S i n 3 0 = x y = S i n N S i n 2 0 , S i n M S i n 3 0 = S i n N S i n 2 0 , ⟹ S i n N S i n ( 1 5 0 − N ) = s i n 2 0 S i n 3 0 . E x p a n d i n g S i n ( 1 5 0 − N ) a n d s i m p l i f y i n g , w e g e t − C o t N + C o t 3 0 = S i n 2 0 1 . Inserting values we finally get N=140. ∴ ∠ P A C = 1 8 0 − 2 0 − 1 4 0 = 2 0 o .
Triangle CAP is isosceles so angle CAP=20 degrees
Why it is isosceles?
What a great solution
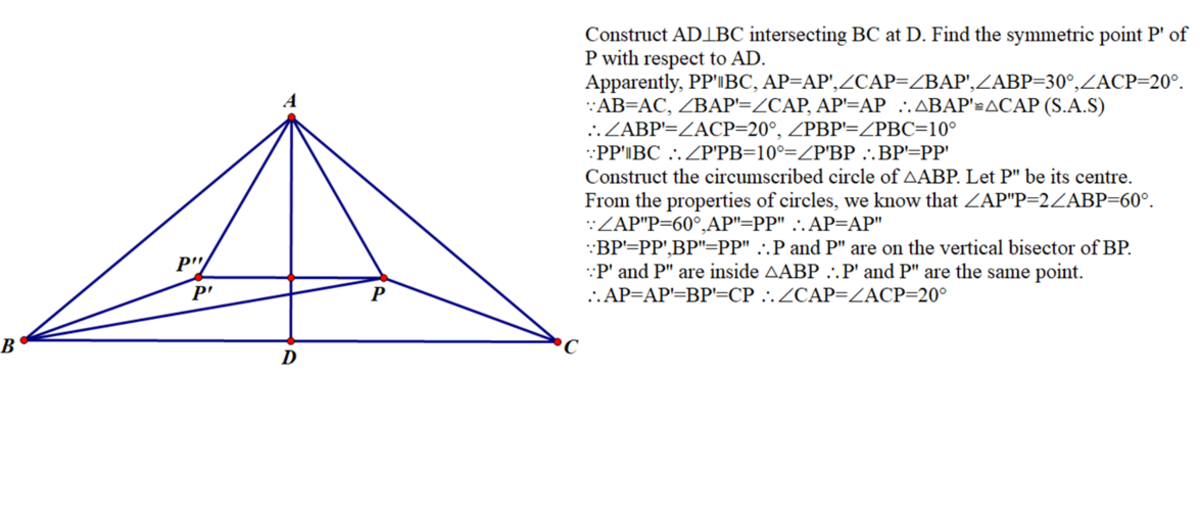
Extend C P and intersects A B at E . Construct E F ⊥ B P intersecting B C at F .
C E bisects ∠ A C B as m ∠ B C P = 2 1 m ∠ B C A . △ A C E ≅ △ F C E ( A . S . A . ), then A C ≅ F C .
Notice m ∠ A E C = 6 0 ° , thus m ∠ F E C = 6 0 ° , then m ∠ B E F = 6 0 ° = m ∠ P E F . E F is both the angle bisector and the height of △ B E P , indicating that △ B E P is isosceles. Therefore, △ B F P is also isosceles. m ∠ P F C = 2 m ∠ P B F = 2 0 ° .
△ A C P ≅ △ F C P ( S . A . S . ), then m ∠ C A P = 2 0 ° .