Drawing some squares

Geometry Level 5

Above is a picture of a 3 × 3 3 \times 3 dot square matrix, which, when the outer dots are connected, form a square. In every vertical and horizontal line that can be drawn on this grid, the dots are equally spaced.

How many distinct squares can be drawn from this grid of nine dots if at least two of the squares' corners are from this grid?


The answer is 70.

Efren Medallo by Efren Medallo , 26, Philippines

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Efren Medallo
Jun 21, 2015

There are 5 kinds of squares that can be drawn from this.

  1. Squares of side 1 1 : There are 12 12 . As a non-obvious example,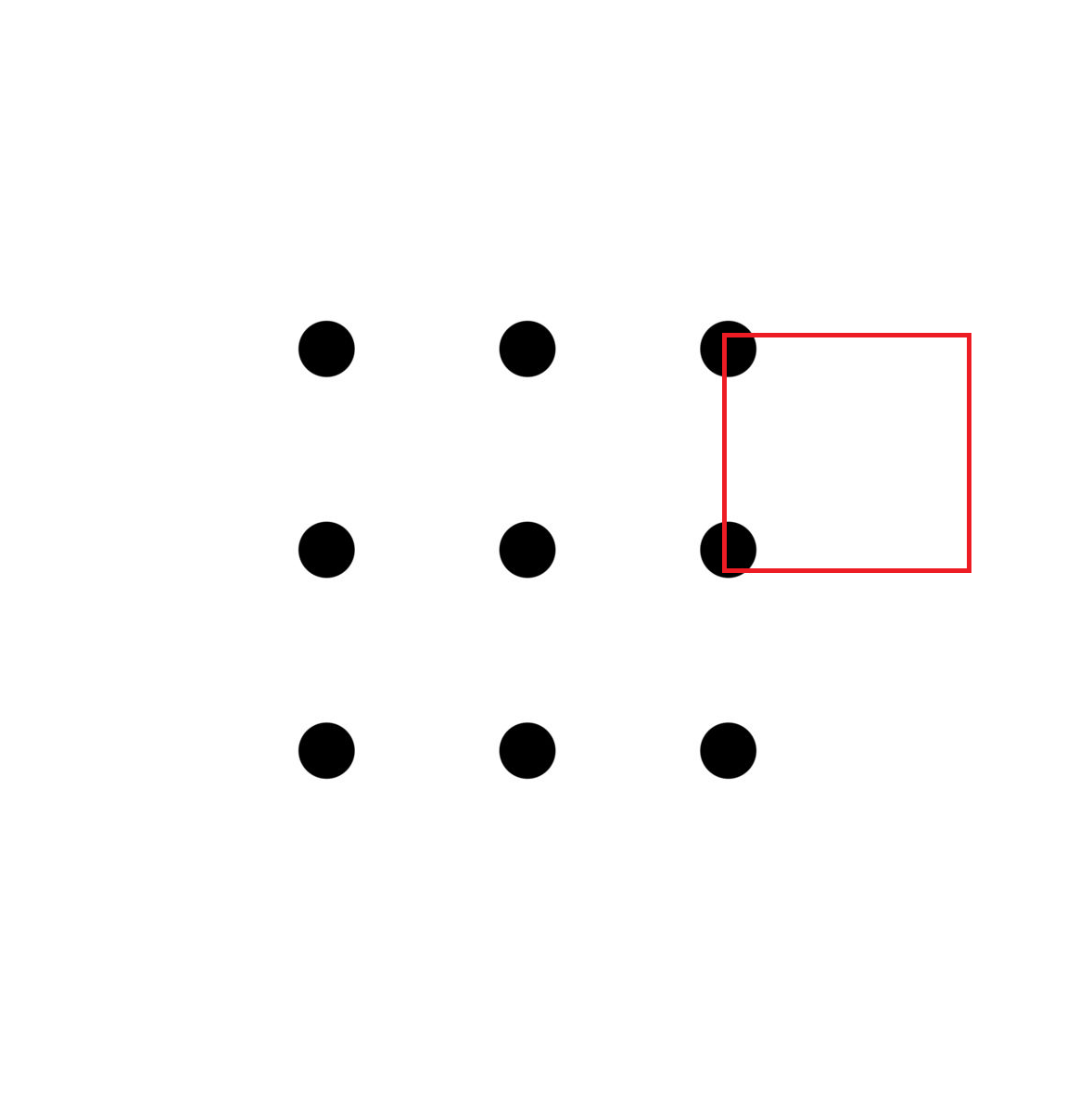

  2. Squares of side 2 2 : There are 9 9 . As a non-obvious example,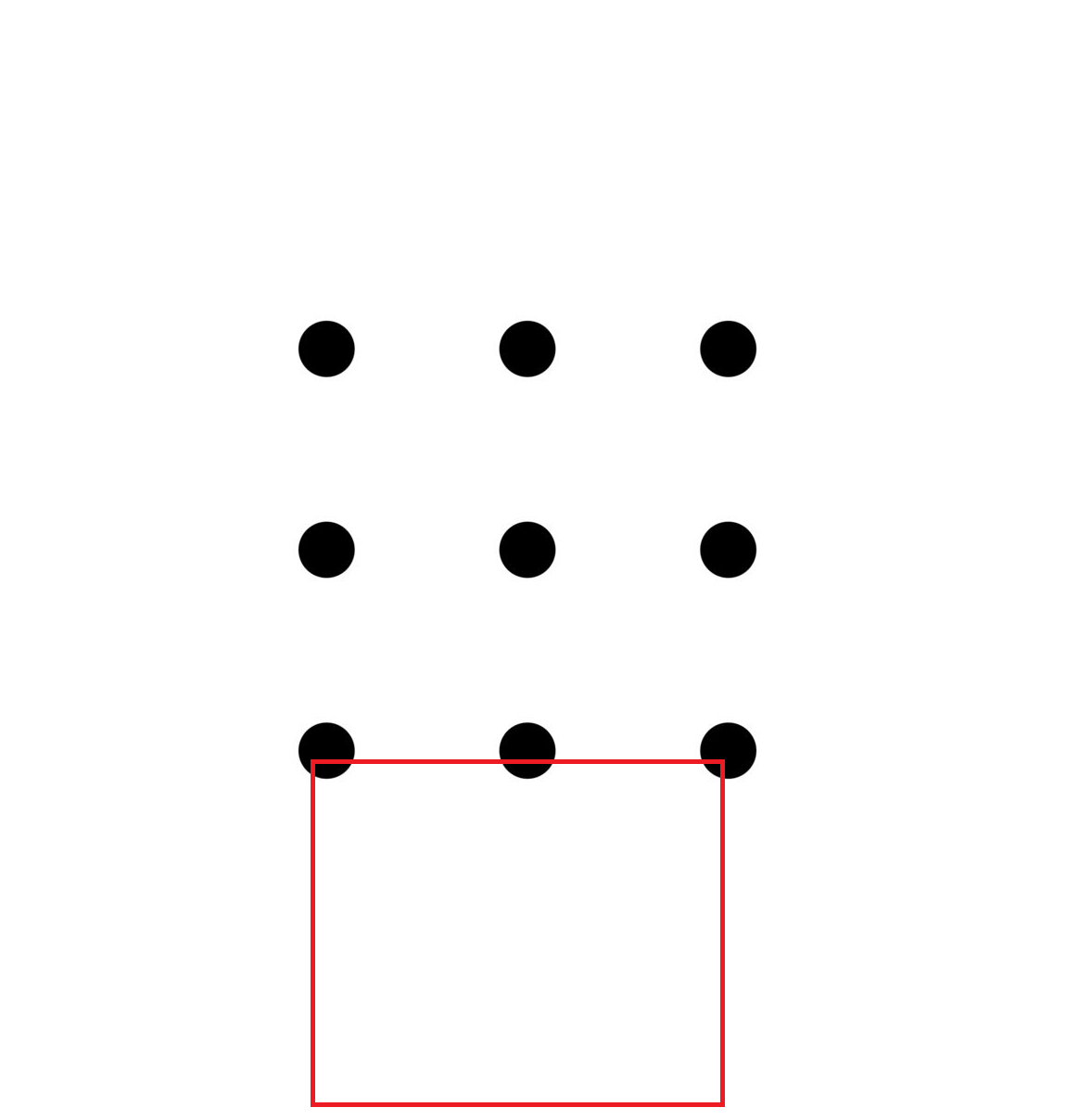

  3. Squares of side 2 \sqrt{2} : There are 9 9 , two of which are depicted here: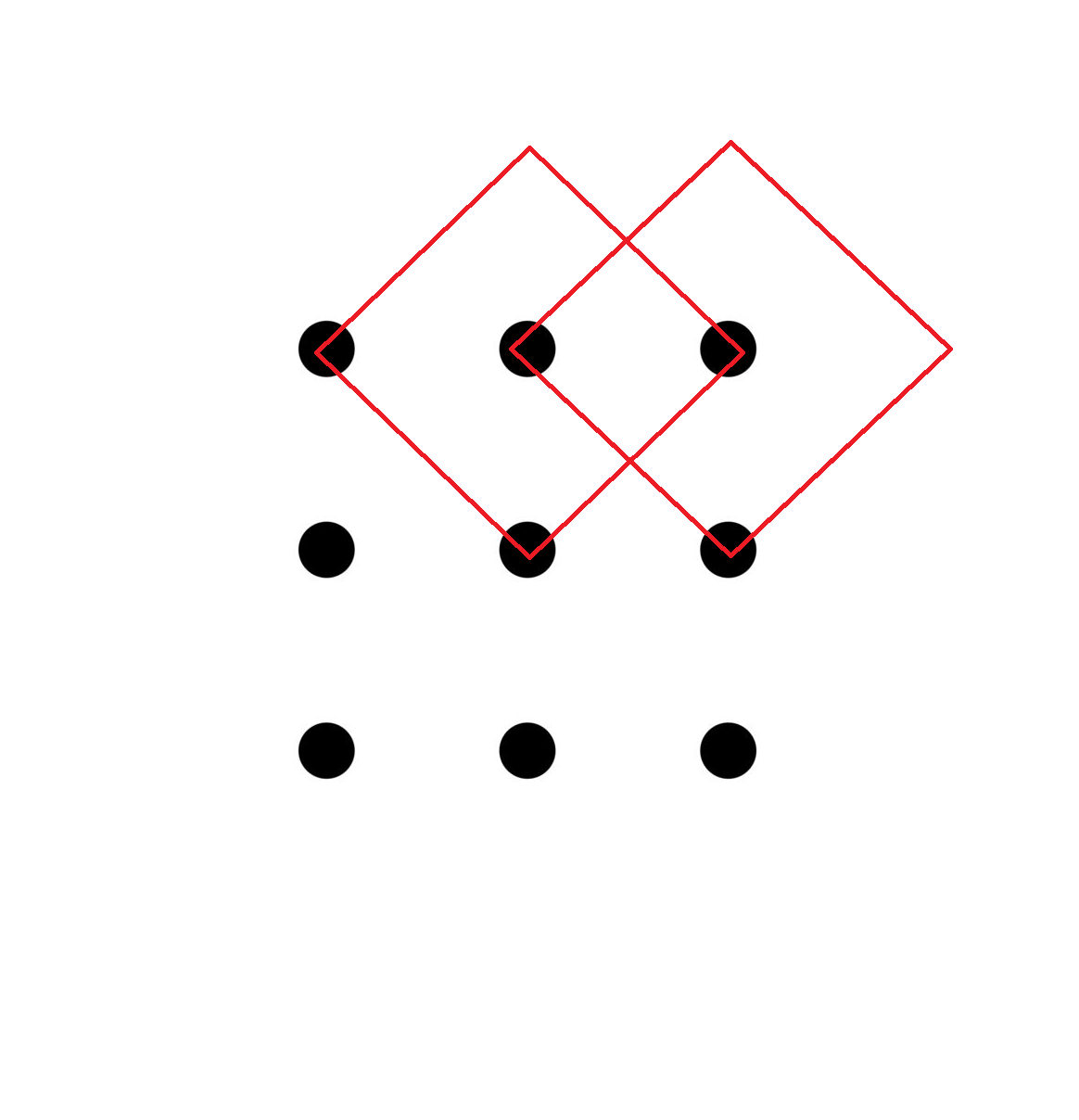

  4. Squares of side 5 \sqrt{5} : There are 16 16 . Notice that every two dot combinations that can make this square can make another one if drawn on the other side.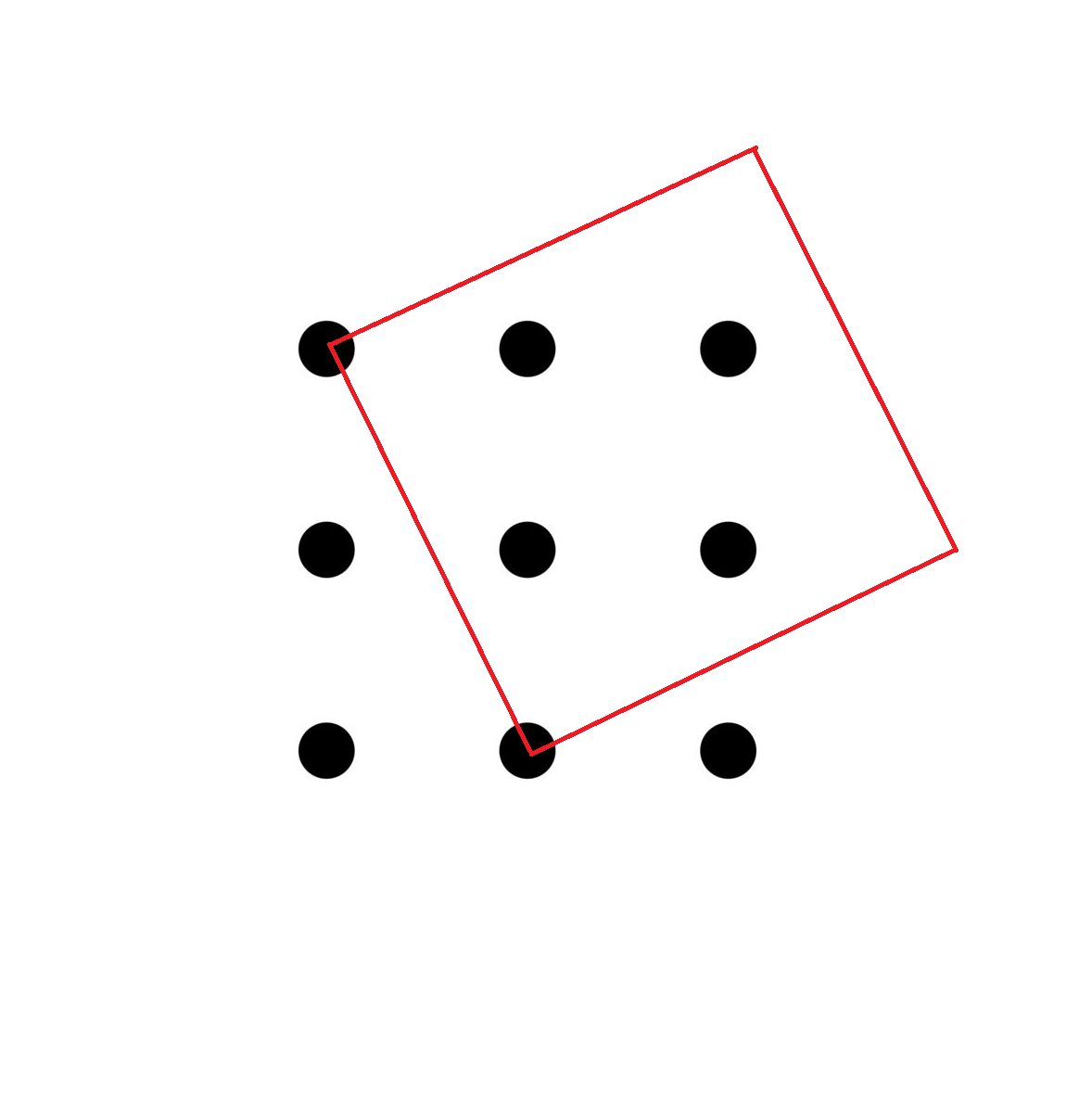

  5. Squares of side 2 2 2\sqrt {2} : There are 4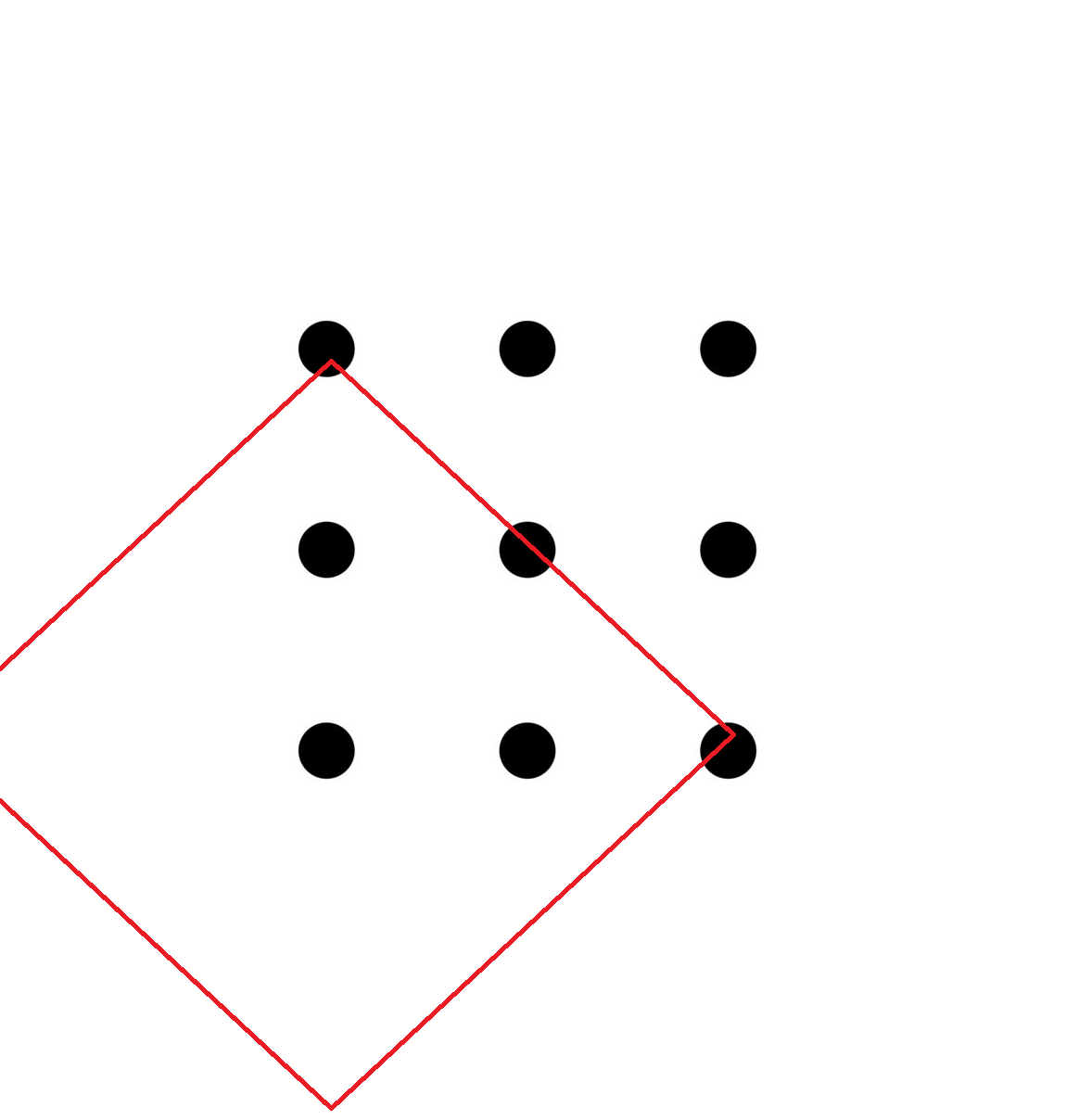 4

That gives a total of 50 50 .

6 Helpful 0 Interesting 0 Brilliant 0 Confused

Beautiful explanation. I had all the pattern but counting was wrong Nice question.

Niranjan Khanderia - 5 years, 11 months ago

Are you sure this isn't a combinatorics problem?

Alex Delhumeau - 5 years, 11 months ago

You missed the squares of side sqrt(2)/2. There are 12 of them. (An example of such a square is the intersection of the two squares of side sqrt(2) in your third drawing.)

Ricardo Moritz Cavalcanti - 5 months, 3 weeks ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...