Dreadful Rotation! 2
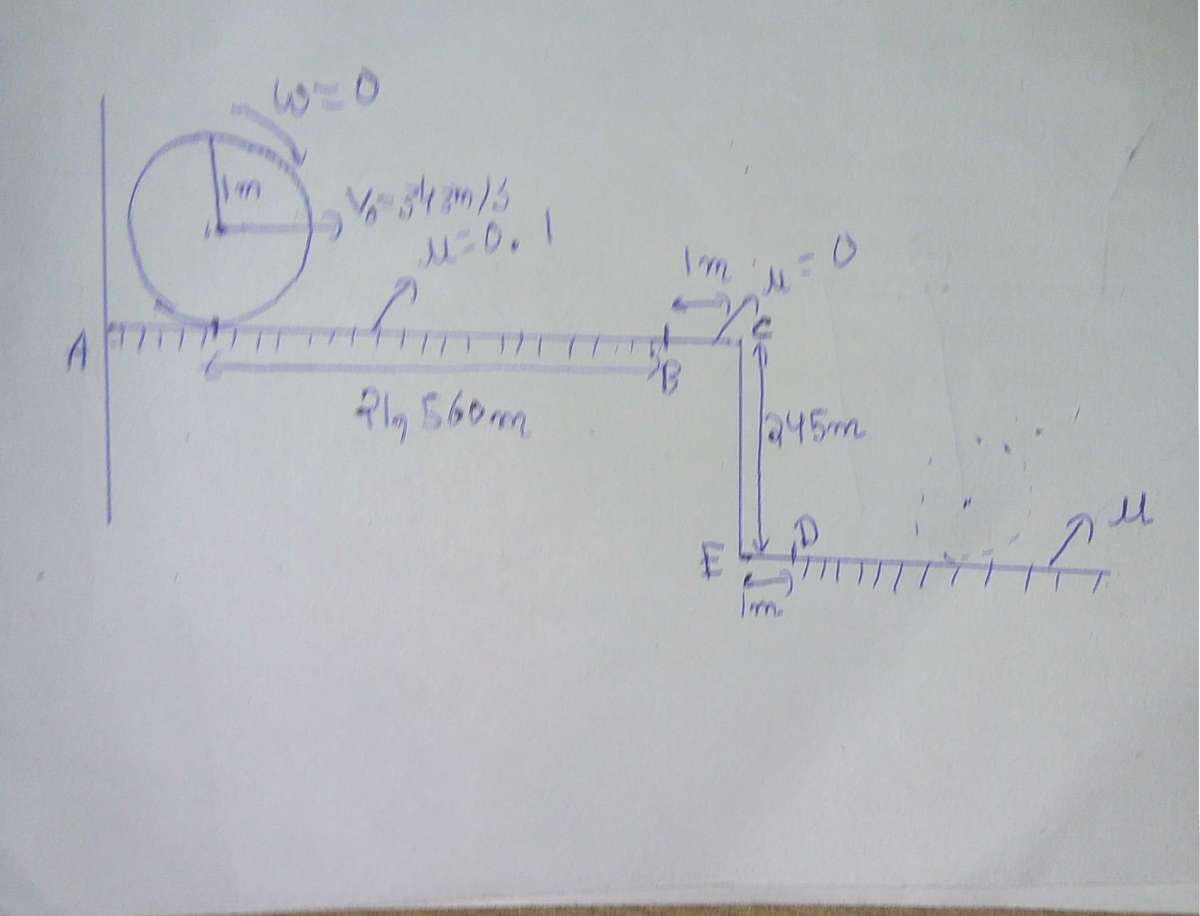
A tennis ball(solid sphere) of mass 1 kg and radius 1 m is sent along surface AB. It moves 21,560m until it reaches B. After that, it rolls on smooth surface BC and loses contact with the top surface. Assuming that as soon as it touches the bottom surface, it starts pure rolling and its vertical velocity component becomes 0, what is the minimum coefficient of friction required to satisfy the requirement.
Details and Assumptions:
-
Height CE=245m
-
Surfaces BC=1m, CE=245m and ED=1m are smooth
-
Ignore air resistance
The answer is 0.4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Initially the ball has no spin, and hence it's point of contact with the supporting surface moves forward, and friction acts in the direction opposite to that of motion. The linear acceleration is 0 . 1 × 1 0 = 1 m/s 2 and the angular acceleration is 2 × 1 5 × 0 . 1 × 1 0 = 2 . 5 rad/s 2 . The time t taken to cover the distance of 2 1 5 6 0 m. is given by 2 1 5 6 0 = 3 4 3 t − 2 1 t 2 ⟹ t 2 − 6 8 6 t + 4 3 1 2 0 = 0 ⟹ t = 7 0 sec. After travelling 2 1 5 6 0 m. , the translational velocity of the C.M. of the ball is 2 7 3 m/s. The angular velocity of the ball is 1 7 5 rad/s. The vertical impulse received by the ball on landing on the bottom surface is J v ^ = 2 × 1 0 × 2 4 5 = 7 0 kg-m/s. The horizontal impulse is given by J h ^ = 2 7 3 − v 1 = 5 2 ω 1 − 7 0 kg-m/s. , where v 1 and ω 1 are the final linear and angular velocities of the ball respectively. With v 1 = ω 1 × r = ω 1 , we get 3 . 5 J h ^ = 9 8 ⟹ J h ^ = 2 8 . For pure rolling to prevail, we must have J h ^ ≤ μ J v ^ ⟹ 2 8 ≤ 7 0 μ ⟹ μ ≥ 7 0 2 8 = 0 . 4