Drilling a cuboid
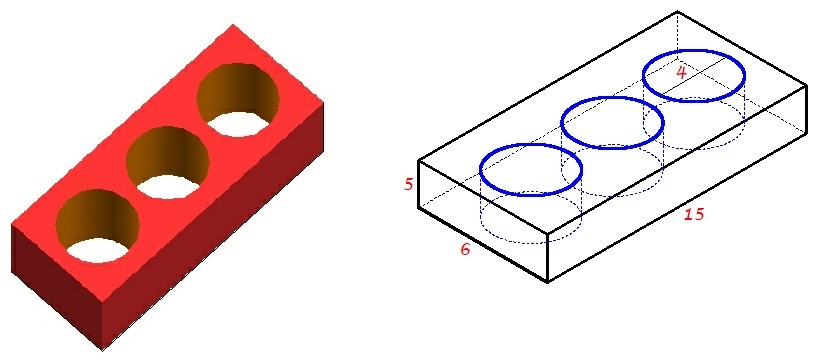 Three identical cylindrical holes each of diameter
has been drilled perpendicular to the base of a
cuboid. Find the surface area of the resulting solid.
Three identical cylindrical holes each of diameter
has been drilled perpendicular to the base of a
cuboid. Find the surface area of the resulting solid.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The surface area of the cuboid is 2 [ 5 ( 1 5 ) + 6 ( 5 ) + 1 5 ( 6 ) ] = 3 9 0
There are three circles at the top and three at the bottom that were removed, and the total area is 6 ( π ) ( 2 2 ) = 2 4 π .
We need to know the lateral area of the three cylindrical holes. We can use the formula, A = c h where c is the circumference of the base and h is the height. So we have, 3 ( 4 π ) ( 5 ) = 6 0 π
The total surface of the new solid is surface area of the cuboid minus the area of the six circles plus the lateral area of the three cylindrical holes. We have
3 9 0 − 2 4 π + 6 0 π = 3 9 0 + 3 6 π