Tilted Drum
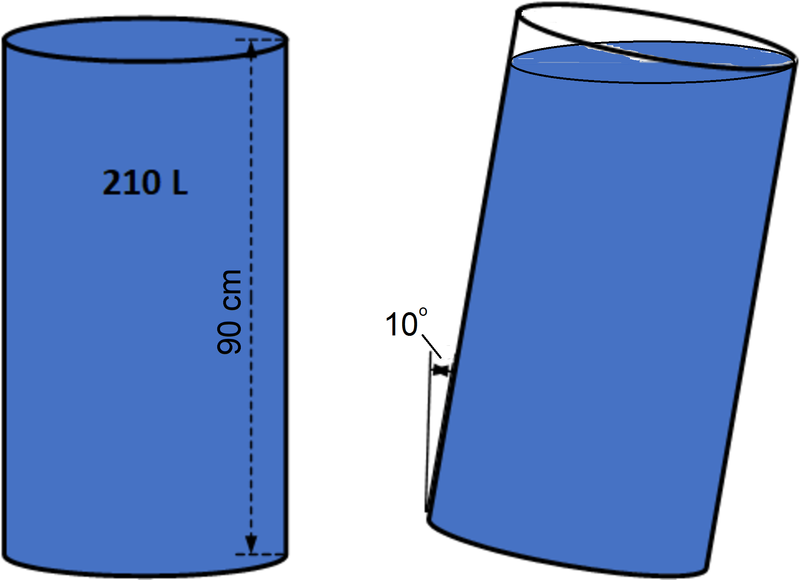
A cylinder drum with an open top and height of 90 cm is filled to the top with 210 L of water. What is the remaining volume of water (in L ) when the drum is tilted 1 0 ∘ with the vertical? (Give your answer to the nearest integer.)
The answer is 199.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Typo in the figure. t a n ( 1 0 ) 2 r
Log in to reply
No, it is correct. 2 r h = tan 1 0 ∘ ⟹ h = 2 r tan 1 0 ∘ . I used this fact in the calculations.
Sorry. I made the mistake because your h and my h are different.
H e i g h t o f w a t e r a t t h e o t h e r e n d h 1 = 9 0 − 2 r ∗ T a n ( 1 0 ) c m .
r
=
9
0
∗
π
2
1
0
0
0
0
=
3
∗
π
7
0
0
0
c
m
.
S
o
w
a
t
e
r
l
e
f
t
=
π
∗
r
2
∗
2
9
0
+
h
1
=
1
/
2
∗
π
∗
7
0
0
0
/
(
3
∗
π
)
∗
(
1
8
0
−
2
∗
7
0
0
0
/
(
3
∗
π
)
∗
T
a
n
(
1
0
)
)
c
m
3
≈
1
9
9
L
V=pi (R^2)[H-2R Tan(x)+R Tan(x)], H=90 R=sqrt[0.21 10^6/(H*pi)]=27.253, x=10 degree V=198.78, Answer=199
We note that the volume of water spilled out Δ V is a half of the volume of a cylinder same radius r as the drum but with a height of 2 r tan 1 0 ∘ . In equation,
Δ V = 2 h 2 r tan 1 0 ∘ V = tan 1 0 ∘ π h 3 1 0 0 0 V 3 = tan 1 0 ∘ π ⋅ 9 0 3 1 0 0 0 ⋅ 2 1 0 3 ≈ 1 1 . 2 where h and V are the height and volume of the drum. Note that r = π h 1 0 0 0 V and V = 2 1 0 and h = 9 0
Therefore the remaining volume of water V − Δ V = 2 1 0 − 1 1 . 2 ≈ 1 9 9 L .