Drunk hexagon
Given a square of side length 1, consider the largest regular hexagon that can be completely inscribed in the square. The diameter of the hexagon can be expressed as a − b , where a and b are positive integers. What is the value of a 2 + b 2 ?
The answer is 40.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
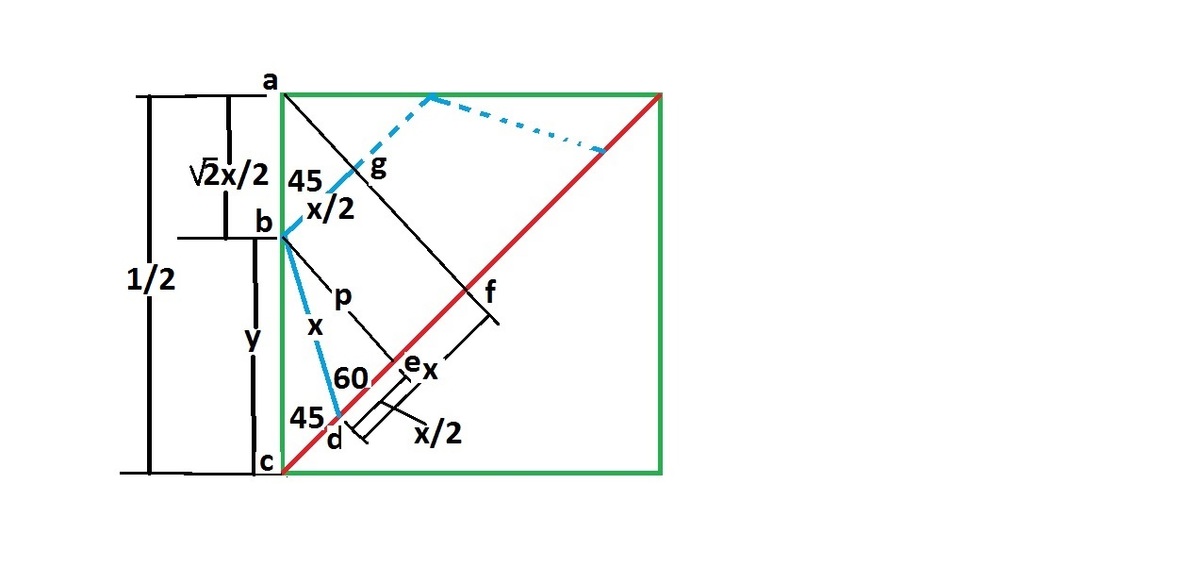
Largest lines in the square and the hexagonal are their diagonals. So the largest hexagon is when the two diagonal coincide. This is shown in one fourth of the sketch above. Half diagonal ’df ’ of the hexagon coincides with half the diagonal ’cf’ of the square. Half hexagon side ’bg’ =x/2 has ’b’ on the square half side ’ac’. ’bd’=x is the hexagon side. From the sketch:- Using the properties of the square and hexagon we have:- p = x S i n 6 0 o = y S i n 4 5 o ⟹ 2 3 x = 2 1 y ∴ b c = y = 2 3 x a n d a b = 2 ∗ 2 x . a c = 2 1 = a b + b c = ( 2 ∗ 2 1 + 2 3 ) ∗ x . ∴ x = 3 + 1 2 . B u t t h e h e x a g o n d i a g o n a l = 2 ∗ d f = 2 x = 2 ∗ 3 + 1 2 . = 6 − 2 = a − b . ∴ a 2 + b 2 = 4 0
Label the center O . Due to the symmetry, the center of the hexagon will be the center of the square. If only 1 diameter of the hexagon is touching the sides of the square, then we could rotate it slightly and expand it, to get a larger hexagon. Hence, 2 diameters of the hexagon must be touching the square.
Split the square up into 4 squares, and the hexagon into 6 equilateral triangles. Consider one of the small squares which contains an equilateral triangle, which has 2 vertices on the perimeter of the original square, and the last vertex is O .
The largest possible side length of this equilateral triangle occurs when it is symmetric about the diagonal of the square from vertex O . This gives us that the side length of the triangle is 2 cos 1 5 1 = 6 + 2 2 = 2 6 − 2 .
Thus, the diameter of the hexagon is 6 − 2 hence a 2 + b 2 = 6 2 + 2 2 = 4 0 .