Duality
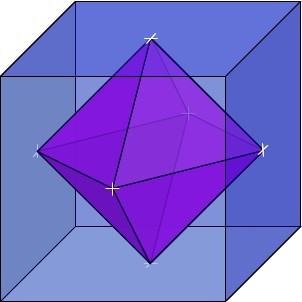 What is the volume of the octahedron inside this
8
in
3
cube?
What is the volume of the octahedron inside this
8
in
3
cube?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
The cube's side is 8 in 3 = 2 in
Let cut the octahedron in two squared pyramids of shared base. Its base is a square formed by join the centers of four adjacent faces of the cube so that the diagonal of the base is 2 in ∴ its area is 2 2 × 2 = 2 (remember: a square is also a rhombus with equal diagonal), also it height is a half of the square's side that is 1 in . Pyramid's volume is 3 b × h ∴ the octahedron's volume is 2 × 3 2 × 1 = 3 4 in 3
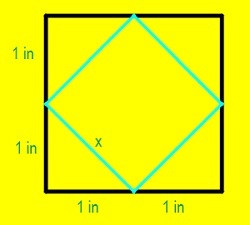 Cube:
Cube:
v = s³
8 = s³
s = 2 inches
Octahedron:
v = 3 1 x 3 2
from the figure
x = 2
v = 3 1 ∗ ( 2 ) 3 ∗ 2
v = 3 4 i n 3
It is not complicated. First, we need to know that a square within a square will have an area of a half of the original square. A pyramid will have a volume one third of the prisim.
Applying these knowledge, we know: A = 8 x 0.5 x (1/3) = (4/3)
That's it.
V=2((1/3)sqrt{2})^2 = (2/3)(2) = 4/3 in^{3}
V = 2 ( 3 1 ) ( 2 ) 2 ( 1 ) = 3 4 .
Note:
The side length of the cube can be computed using the formula, V = a 3 , where V is the volume and a is the edge length. The edge length is 2 .