Dubai Towers Perspective
An aerial shot is made of three Dubai towers and their spires.

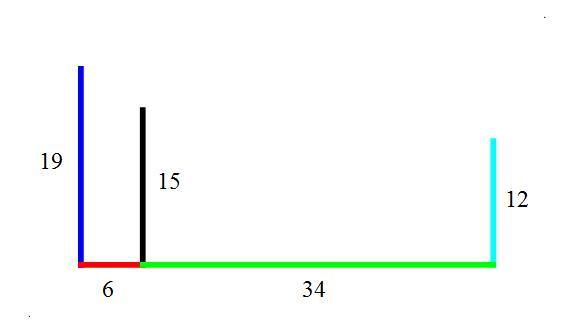
Measurement of the photograph shows that the distances from the horizon line to the top of the spires and distances between the vertical lines through the spires are in the ratios as shown in this graphic
It is known from public records that relative to a surveyor's benchmark nearby, the coordinates of the top of the three spires are, in feet
The shot was made horizontal, so that vertical lines in the landscape appear as vertical lines in the photograph. But the shot was made feet above the ground. That is, at the time of the shot, the camera was at, in feet, relative to the same benchmark
Find , in feet
Note: Disregard the curvature of the Earth. Also, assume ideal pinhole optics and flat film plate. Not a "swept panorama shot". Also, solution is unique.
The answer is 255.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Check out this graphic
Plotted in this 3D graphic are the coordinates of the of the three towers and their spires, the camera's coordinates ( − 3 1 0 , − 3 7 0 , 2 5 5 ) , as well as an image plane, where the horizon line is at z = 2 5 5 and the coordinates of the same three towers in the image plane, which are
( 5 0 , 1 5 0 , 3 8 0 + 2 5 5 )
( 1 2 2 , 5 4 , 3 0 0 + 2 5 5 )
( 5 3 0 , − 4 9 0 , 2 4 0 + 2 5 5 )
the horizontal distances between the verticals of the image plane being exactly 1 2 0 and 6 8 0 collinearly. Hence, the vertical lengths and distances between them
( 3 8 0 , 1 2 0 , 3 0 0 , 6 8 0 , 2 4 0 )
has the ratios as per the graphic of measurements
( 1 9 , 6 , 1 5 , 3 4 , 1 2 )
Hence, the answer is z = 2 5 5 feet.
The image plane can be arbitrarily scaled relative to the camera's coordinates, with one particular scale chosen for clarity of the 3D graphic. The image plane cannot be assumed to be parallel to the towers because the towers are not necessarily coplanar. In fact, if the towers were coplanar, we would lack sufficient information to be able to uniquely determine the coordinates of the camera.
The camera has 4 degrees of freedom, which is ( x , y , z , θ ) , θ being the direction of the shot. Hence, given 3 towers, the appearance of the towers in the photograph has 4 degrees of freedom, which is exemplified by the graphic of relative measurements, i.e., there are 4 independent ratios, since the scaling factor is arbitrary. Unless the towers are coplanar which introduces degeneracy, the solution is [locally,i.e. about where as suggested in the photograph] unique, and in this case exact.