Dubya part 2
When is graphed, all areas below and on/above the curve are shaded. If the area of the shaded region is , find .
Notations :
-
denotes the absolute value function .
-
denotes the floor function .
The answer is 2750.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The simplest way to solve this problem is to graph y = 7 (blue) and y = ∣ x ∣ + 2 ∣ x + 1 ∣ − 3 ∣ x + 2 ∣ + 4 ∣ x + 3 ∣ (red). This is how it looks: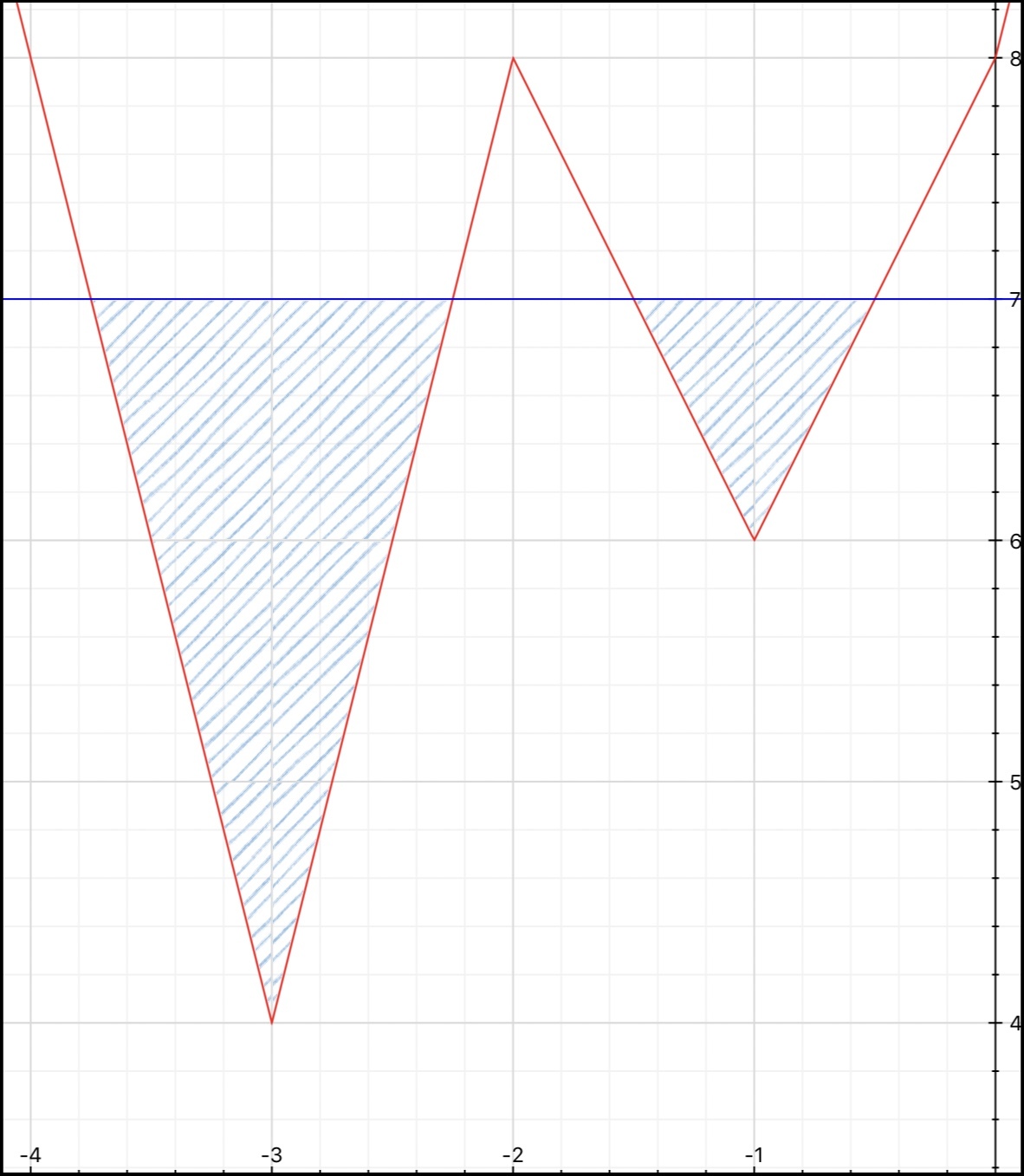 The shaded areas are the ones we’re looking for. The first (bigger) one is a triangle with height 3 and base 1.5, and the other has base 1 and height 1. Their areas are 2.25 and 0.5, total 2.75. Therefore
ε
=
2
.
7
5
. Multiplied by 1000 this becomes 2750 which is our solution.
(The floor function won’t do anything to an integer so we can just skip it.)
The shaded areas are the ones we’re looking for. The first (bigger) one is a triangle with height 3 and base 1.5, and the other has base 1 and height 1. Their areas are 2.25 and 0.5, total 2.75. Therefore
ε
=
2
.
7
5
. Multiplied by 1000 this becomes 2750 which is our solution.
(The floor function won’t do anything to an integer so we can just skip it.)