Duck and Fox
A duck is in the center of a circular pond. The duck wants to swim ashore, because it wants to fly off and this particular duck is not able to start flying from the water.
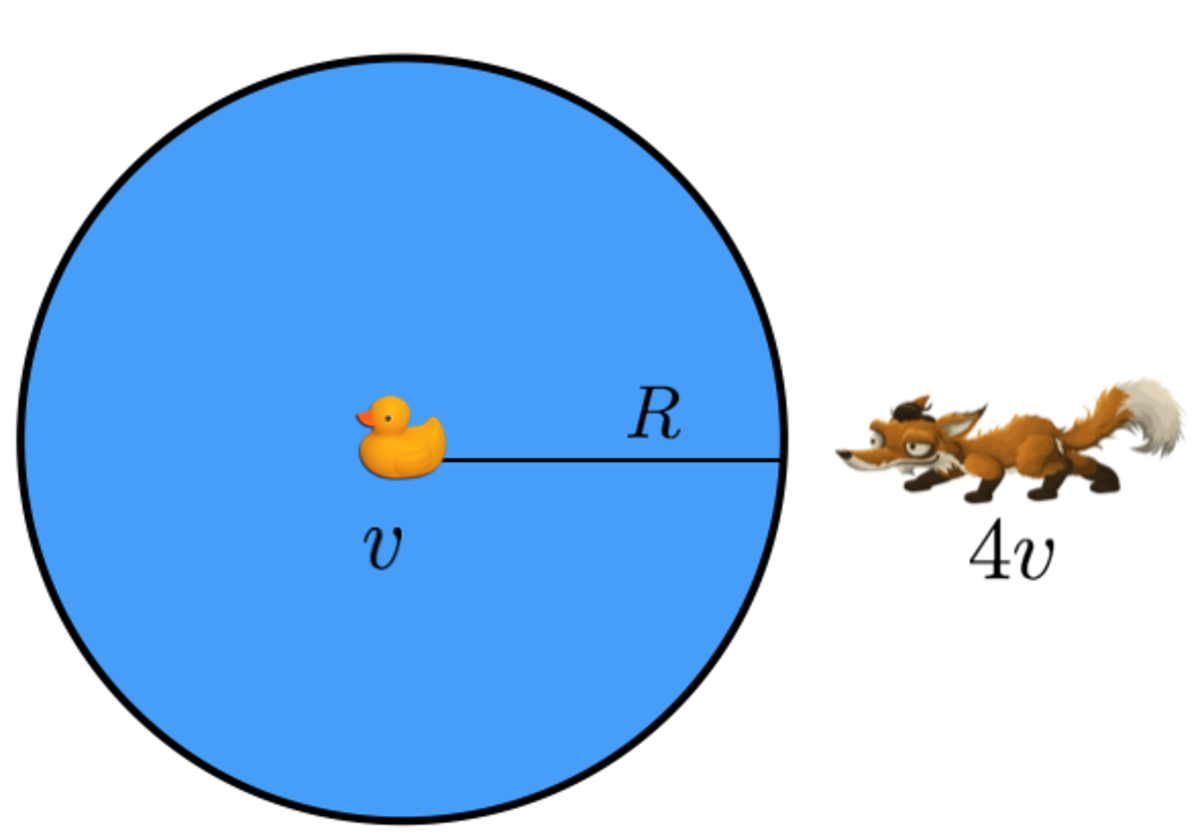
There is also a fox, on the shore. The fox wants to eat the duck, but this particular fox cannot swim, so it can only hope to catch the duck when the duck reaches the shore.
The fox can run times faster than the duck can swim. Is there a way for the duck to escape?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The duck could swim in concentric circles, so that the fox has to continuously run along the circumference of the pond to stay on the same radius as the duck. If the duck swims near the edge of the pond, the fox could easily keep up since they would be covering approximately the same distance and the fox is four times faster. But what if the duck swam closer to the center of the pond? The duck would have to cover a smaller circumference, and could use this strategy to put some distance between the fox and itself. At a distance of r / 4 from the center of the pond, the circumference of the pond is exactly four times the circumference of the duck’s path. Thus, to stay on the same radius as the duck, the fox would barely keep up.
Say, the duck circles the pond at a distance r / 4 − e , where e is an infinitesimal amount. So as the duck continues to swim along this radius, it would slowly gain some distance over the fox. Once the duck is able to gain 1 8 0 degrees over the fox, the duck would have to cover a distance of 3 r / 4 + e to reach the edge of the pond. In the meanwhile, the fox would have to cover half the circumference of the pond (i.e the 1 8 0 degrees). At that point,
( π r ) > 4 ( 3 r / 4 + e )
The duck would be able to make it to land and fly away.